题目内容
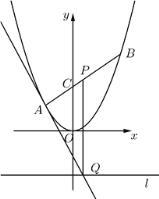
【题目】如图,在平面直角坐标系![]() 中,过
中,过![]() 轴正方向上一点
轴正方向上一点![]() 任作一直线,与抛物线
任作一直线,与抛物线![]() 相交于
相交于![]() 两点,一条垂直于
两点,一条垂直于![]() 轴的直线分别与线段
轴的直线分别与线段![]() 和直线
和直线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 与该抛物线有且仅有一个公共点.
与该抛物线有且仅有一个公共点.
(3)若直线![]() 的斜率存在,且与该抛物线有且仅有一个公共点,试问
的斜率存在,且与该抛物线有且仅有一个公共点,试问![]() 是否一定为线段
是否一定为线段![]() 的中点?说明理由.
的中点?说明理由.
【答案】(1)![]() .(2)见解析(3)
.(2)见解析(3)![]() 是
是![]() 的中点.见解析
的中点.见解析
【解析】
(1)联立方程利用韦达定理得到![]() ,
,![]() ,再根据
,再根据![]() ,计算得到答案.
,计算得到答案.
(2)计算![]() .
.![]() ,设
,设![]() 在
在![]() 上, 且满足
上, 且满足![]() ,故
,故![]() , 与
, 与![]() 联立得
联立得![]() , 得到答案.
, 得到答案.
(3)设![]() ,计算得到
,计算得到![]() ,
,![]() ,
,![]() . 与
. 与![]() 联立得到
联立得到![]() 得到答案.
得到答案.
(1) 设![]() ,与
,与![]() 联立, 得
联立, 得![]() . 故
. 故![]()
从而![]() ,根据解
,根据解![]() 得到
得到![]() 得
得![]() 或
或![]() ,
,
舍去负值, 得![]() .
.
(2) ![]() , 故
, 故![]() .
.![]() .
.
设![]() 在
在![]() 上, 且满足
上, 且满足![]() .
.
![]() , 故直线
, 故直线![]() 的方程为
的方程为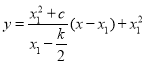 ,
,
而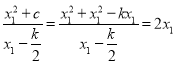 .
.
故![]() , 与
, 与![]() 联立得
联立得![]() ,
,
故直线![]() 与该抛物线有且仅有一个公共点.
与该抛物线有且仅有一个公共点.
(3) 设![]() , 这里
, 这里![]() , 由(2)知过
, 由(2)知过![]() 的与
的与![]() 有且仅有一个公共点的斜率存在的直线必为
有且仅有一个公共点的斜率存在的直线必为![]() .与
.与![]() 相交, 得
相交, 得![]() .
.
故![]() .
. ![]() , 所以
, 所以![]() . 与
. 与![]() 联立,
联立,
得![]() , 即
, 即![]() , 故
, 故![]() .
.
这样![]() , 即
, 即![]() 是
是![]() 的中点.
的中点.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目