题目内容
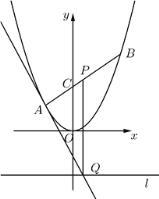
【题目】已知点P(1,2)在抛物线C:y2=2px(p>0)上.
(Ⅰ)求C的方程;
(Ⅱ)斜率为﹣1的直线与C交于异于点P的两个不同的点M,N,若直线PM,PN分别与x轴交于A,B两点,求证:△PAB为等腰三角形.
【答案】(Ⅰ) y2=4x; (Ⅱ)见解析
【解析】
(Ⅰ) 将点P(1,2)代入抛物线方程可得结果；
(Ⅱ) 设直线MN的方程为y=﹣x+t,联立抛物线方程y2=4x，根据韦达定理和斜率公式运算可得.
(Ⅰ)将点P(1,2)代入抛物线方程可得22=2p1,∴p=2,所以抛物线方程为y2=4x;
(Ⅱ)证明:由题意设直线MN的方程为y=﹣x+t,联立抛物线方程y2=4x,可得x2﹣(2t+4)x+t2=0,
设M(x1,y1),N(x2,y2),可得x1+x2=2t+4,x1x2=t2,
由kPM+kPN
2+(t﹣3)(
)
=﹣2+(t﹣3)
2+2(t﹣3)
0,
则∠PAB=∠PBA,即△PAB为等腰三角形.
练习册系列答案
相关题目
