题目内容
【题目】已知椭圆C:![]() l(a>b>0)经过点(
l(a>b>0)经过点(![]() ,1),且离心率e
,1),且离心率e![]() .
.
(1)求椭圆C的方程;
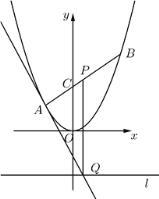
(2)若直线l与椭圆C相交于AB两点,且满足∠AOB=90°(O为坐标原点),求|AB|的取值范围.
【答案】(1)![]() ;(2)[
;(2)[![]() ,2
,2![]() ].
].
【解析】
(1)点的坐标代入可得一个关系式![]() ,离心率得
,离心率得![]() ,结合
,结合![]() 可求得
可求得![]() ,得椭圆方程;
,得椭圆方程;
(2)当直线l的斜率不存在时, 设直线l为:x=m,代入计算![]() ,当直线的斜率存在时,设直线为:y=kx+m,A(x,y),B(
,当直线的斜率存在时,设直线为:y=kx+m,A(x,y),B(![]() ,
,![]() ),代入椭圆中整理,由韦达定理得
),代入椭圆中整理,由韦达定理得![]() ,代入
,代入![]() 得出
得出![]() 的关系,计算
的关系,计算![]() ,用换元法转化为求二次函数的取值范围得出结论.
,用换元法转化为求二次函数的取值范围得出结论.
(1)由题意:e![]() ,
,![]() 1,a2=b2+c2,解得:a2=8,b2=4,所以椭圆的方程为:
1,a2=b2+c2,解得:a2=8,b2=4,所以椭圆的方程为:![]() ;
;
(2)当直线l的斜率不存在时,设直线l为:x=m,A(x,y),B(![]() ,
,![]() ),代入椭中:y2=4(1
),代入椭中:y2=4(1![]() ),
),
∠AOB=90°,∴![]() 0,∴x
0,∴x![]() +y
+y![]() =m2﹣4(1
=m2﹣4(1![]() )=0,∴m2
)=0,∴m2![]() ,
,
∴|AB|=|y﹣![]() |=4
|=4![]() ;
;
当直线的斜率存在时,设直线为:y=kx+m,A(x,y),B(![]() ,
,![]() ),代入椭圆中整理得:
),代入椭圆中整理得:
(1+2k2)x2+4kmx+2m2﹣8=0,
x+![]()
![]() ,x
,x![]()
![]() ,
,![]() =k2xx'+km(x+
=k2xx'+km(x+![]() )+m2
)+m2![]() ,
,
∵∠AOB=90°,∴x![]() +y
+y![]() =0,∴2m2﹣8+m2﹣8k2=0,∴3m2=8+8k2,
=0,∴2m2﹣8+m2﹣8k2=0,∴3m2=8+8k2,
|AB|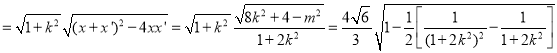 ,
,
令t![]() ∈(0,1],所以|AB|
∈(0,1],所以|AB|![]() ,
,
当t![]() ,g(t)=1
,g(t)=1![]() (t2﹣t)最大为
(t2﹣t)最大为![]() ,t=1时,g(t)取得最小值1,
,t=1时,g(t)取得最小值1,
综上所述:|AB|的取值范围[![]() ,2
,2![]() ].
].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目