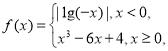Question

【题目】已知函数.

（Ⅰ）若为的极值点，求实数的值；

（Ⅱ）若在上为增函数，求实数的取值范围；

（III）当时，方程有实根，求实数的最大值.

Answer 1

【答案】（I）；（II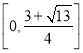）；（III）.

【解析】

试题分析：（I）借助题设条件运用极值的定义建立方程求解；（II）借助题设运用分类整合的数学思想分析推证；（III）依据题设构造函数运用导数的知识探求.

试题解析：

（I）

因为为的极值点，所以，即，解得。

（II）因为函数在上为增函数，所以

在上恒成立。

当时，在上恒成立，所以在上为增函数，故 符合题意。

当时，由函数的定义域可知，必须有对恒成立，故只能，所以在上恒成立。

令函数，其对称轴为，因为，所以，要使在上恒成立，只要即可，即，所以。因为，所以。

综上所述，a的取值范围为。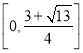

（Ⅲ）当时，方程可化为。

问题转化为在上有解，即求函数的值域。

因为函数，令函数，

则，

所以当时，，从而函数在上为增函数，

当时，，从而函数在上为减函数，

因此。

而，所以，因此当时，b取得最大值0.