题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)是否存在实数![]() ,使
,使![]() 恒成立,若存在,求出实数
恒成立,若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ,当
,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数的知识;(2)借助题设运用导数的知识求解探求.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,
由![]() ,得
,得![]() ,或
,或![]() ,
,
由![]() ,得
,得![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
故函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]() 恒成立等价于
恒成立等价于![]() 恒成立,
恒成立,
令![]() ,
,
当![]() 时,即当
时,即当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 内不能恒成立,
内不能恒成立,
当![]() 时,即当
时,即当![]() 时,则
时,则![]() ,
,
故![]() 在
在![]() 内不能恒成立,
内不能恒成立,
当![]() 时,即当
时,即当![]() 时,
时,
![]() ,
,
由![]() 解得
解得![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() ,
,
解得![]() .
.
综上,当![]() 时,
时,![]() 在
在![]() 内恒成立,即
内恒成立,即![]() 恒成立,
恒成立,
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 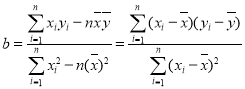 ,
, ![]() .
.