题目内容
【题目】已知
为等差数列，且
，
.
（1）求的通项公式；
（2）若等比数列
满足
，
，求的前
项和公式.
【答案】(1)
；（2）
.
【解析】
试题分析：（1）设出等差数列的公差为
，然后根据第三项为
，第六项为
利用等差数列的通项公式列出方程解出
和
即可得到数列的通项公式；（2）根据
和
的通项公式求出
，因为
为等比数列，可用
求出公比，然后利用首项和公比写出等比数列的前
项和的公式.
试题解析：(1)设等差数列{an}的公差为d.
因为a3＝－6，a6＝0，
所以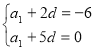
解得a1＝－10，d＝2.
所以an＝－10＋(n－1)×2＝2n－12.
(2)设等比数列{bn}的公比为q.
因为b2＝a1＋a2＋a3＝－24，
，
所以－8q＝－24，q＝3.
所以数列{bn}的前n项和公式为
Sn＝
．
练习册系列答案
相关题目
【题目】为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》，全面提高我市中学生的体质健康水平，普及足球知识和技能，市教体局决定矩形春季校园足球联赛，为迎接此次联赛，甲同学选拔了20名学生组成集训队，现统计了这20名学生的身高，记录如下表：
身高（ | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
（1）请计算这20名学生的身高中位数、众数，并补充完成下面的茎叶图；
（2）身高为185
和188
的四名学生分别为
，
，
，
，先从这四名学生中选2名担任正副门将，请利用列举法列出所有可能情况，并求学生
入选正门将的概率．
