题目内容
【题目】直线![]() 过点
过点![]() ,与
,与![]() 轴,
轴,![]() 轴的正半轴分布交于
轴的正半轴分布交于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)当直线![]() 的斜率
的斜率![]() 时,求
时,求![]() 的外接圆的面积;
的外接圆的面积;
(2)当![]() 的面积最小时,求直线的方程.
的面积最小时,求直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:对问题(1),首先根据题目条件求出直线的方程,在此基础上求出直角三角形![]() 的斜边长,即
的斜边长,即![]() 的外接圆的直径,进而可求出
的外接圆的直径,进而可求出![]() 的外接圆的面积;对于问题(2),首先设出直线的方程,并用斜率
的外接圆的面积;对于问题(2),首先设出直线的方程,并用斜率![]() 表示出
表示出![]() 的面积,再结合基本不等式可求出
的面积,再结合基本不等式可求出![]() 的面积最小时斜率
的面积最小时斜率![]() 的值,进而可求得直线的方程.
的值,进而可求得直线的方程.
试题解析:(1)由题知直线![]() 的方程为
的方程为![]() ,即
,即![]() .............2分
.............2分
可知![]() ,..................3分
,..................3分
且![]() 是直角三角形,
是直角三角形,![]() 为斜边,故
为斜边,故![]() 的外接圆半径
的外接圆半径![]() ..............4分
..............4分
所以外接圆的面积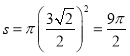 ......................5分
......................5分
(2)由题知直线![]() 的斜率
的斜率![]() 存在,且
存在,且![]() ,设直线
,设直线![]() ,
,
令![]() ;令
;令![]() ,......................7分
,......................7分
![]() ,
,
由勾函数知,当![]() 时,
时,![]() 最小..................9分
最小..................9分
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ....................10分
....................10分

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目