题目内容
【题目】我国某沙漠，曾被称为“死亡之海”，截止2018年年底该地区的绿化率只有
，计划从2019年开始使用无人机飞播造林，弹射的种子可以直接打入沙面里头，实现快速播种，每年原来沙漠面积的
将被改为绿洲，但同时原有绿洲面积的
还会被沙漠化。设该地区的面积为
，2018年年底绿洲面积为
，经过一年绿洲面积为
……经过
年绿洲面积为
，
（1）求经过年绿洲面积；
（2）截止到哪一年年底，才能使该地区绿洲面积超过
？（取
）
【答案】(1) 
(2) 2022年年底
【解析】
（1）根据“每年原来沙漠面积的
将被改为绿洲，但同时原有绿洲面积的
还会被沙漠化”写出数。列
的递推关系式，然后利用配凑法配成等比数列，并由此求得数列的通项公式.（2）令
，解指数不等式求得
的取值范围，并根据的最小值求得截止的年份.
解：（1）由题：
，所以
，而
，故
.
（2）
，得
，所以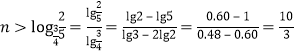
所以
，即截止到2022年年底.
练习册系列答案
相关题目
【题目】某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；
(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；
(3)求续保人本年度平均保费的估计值．
