��Ŀ����
����Ŀ��ijѧУΪ���������ѧ�����������������������ķ�����ȡ80��ѧ�����õ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1������Ů�����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��2��������֪ͼ��1����������170��175cm������������16�ˣ�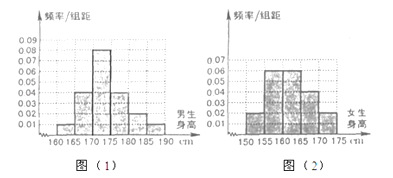
���������ڳ�ȡ��ѧ���У��С�Ů�����ж����ˣ�
������Ƶ�ʷֲ�ֱ��ͼ��������е�2��2�����������ж����ж�ٷּ����İ�����Ϊ���������Ա��йء���
��170cm | ��170cm | �ܼ� | |
�������� | |||
������ | |||
�ܼ� |
����������80��ѧ���У���������170��175cm֮���ѧ���а��С�Ů�Ա�ֲ�����ķ��������5�ˣ�����5����ѡ��3�˵����֣���3����ǡ����һ��Ů���ĸ��ʣ�
�ο���ʽ��K2=![]()
�ο����ݣ�
P��K2��k0�� | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡��⣺����ֱ��ͼ�У�
��������170��175cm��������Ƶ��Ϊ0.08��5=0.4��
��������Ϊn1 �� ��0.4=![]() ����n1=40��
����n1=40��
������������Ϊ40����Ů��������Ϊ80��40=40��
�����������ߡ�170cm������=��0.08+0.04+0.02+0.01����5��40=30��Ů�����ߡ�170cm������0.02��5��40=4�����Կɵõ�������������
��170cm | ��170cm | �ܼ� | |
�������� | 30 | 10 | 40 |
������ | 4 | 36 | 40 |
�ܼ� | 34 | 46 | 80 |
������99.9%�İ�����Ϊ�������Ա��йأ�
������170��175cm֮���������16�ˣ�Ů��������4�ˣ�
���ֲ�����ķ������5�ˣ�������ռ4�ˣ�Ů��ռ1�ˣ�
������ΪA1 �� A2 �� A3 �� A4 �� Ů��ΪB��
��5����ѡ3���У���A1 �� A2 �� A3������A1 �� A2 �� A4������A1 �� A2 �� B������A1 �� A3 �� A4������A1 �� A3 �� B������A1 �� A4 �� B������A2 �� A3 �� A4������A2 �� A3 �� B����
��A2 �� A4 �� B������A3 �� A4 �� B������10�ֿ��ܣ�
3����ǡ����һ��Ů���У���A1 �� A2 �� B������A1 �� A3 �� B������A1 �� A4 �� B������A2 �� A3 �� B������A2 �� A4 �� B������A3 �� A4 �� B������6�ֿ��ܣ�
���������Ϊ![]() ��
��
��������������ֱ��ͼ��������170��175cm��������Ƶ��Ϊ0.08��5=0.4���ɵ�������Ϊ40��������������Ϊ40����Ů��������Ϊ80��40=40��
��������������ߡ�170cm��������Ů�����ߡ�170cm���������õ�2��2�����������k2 �� ��𰸿���
���������170��175cm֮���������16�ˣ�Ů��������4�ˣ����ɷֲ�����ķ������5�ˣ��õ�����ռ4�ˣ�Ů��ռ1�ˣ�Ȼ������ö�ٷ��õ�ѡ��3�˵ķ������������3����ǡ����һ��Ů�������������ùŵ����ģ�ͼ��㹫ʽ�ô𰸣�
�����㾫����������Ҫ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ������ȷ�����⣮