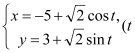题目内容
【题目】
为原点的直角坐标系中，点
为
的直角顶点，已知
，且点
的纵坐标大于0．
(1)求
的坐标；
(2)求圆
关于直线
对称的圆
的方程；在直线上是否存在点
，过点的任意一条直线如果和圆
圆都相交，则该直线被两圆截得的线段长相等，如果存在求出点的坐标，如果不存在，请说明理由.
【答案】(1)
；(2)
，存在点
.
【解析】
试题分析：(1)设出要求的向量的坐标,根据所给的模长的关系和直角三角形两条直角边垂直的关系,写出关于向量坐标的关系式,解方程,舍去不合题意的结果,得到向量的坐标；(2)要求圆关于直线的对称圆,只要求出圆心关于直线的对称点即可.本题需要先根据向量的坐标求出点
的坐标,从而求出直线的方程,通过计算得到结果.
试题解析：(1)设
，由
...........1分
得
，解得
或
...........3分
若，则
与
矛盾
若，则
符合，即...........4分；
(2)
，所以
...........6分
直线
的方程为
...........8分
设
则
所以圆
的方程为...........10分
存在点，根据图形的对称性，点即为线段
的中点，坐标为...........12分.
练习册系列答案
孟建平名校考卷系列答案
相关题目
