题目内容
【题目】已知函数![]() .
.
(I)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(II)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方,求
下方,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)求导再由![]()
![]()
![]()
![]()
![]()
![]() 切线方程得:
切线方程得:![]()
![]()
![]() ;(II)令
;(II)令![]() ,再利用转化思想将原命题等价转化为
,再利用转化思想将原命题等价转化为![]() 在区间
在区间![]() 上恒成立.然后利用分类讨论思想,并借助导数工具,求得:当
上恒成立.然后利用分类讨论思想,并借助导数工具,求得:当![]() 时,函数
时,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方.
下方.
试题解析:(I)由题知,![]() ,………………1分
,………………1分
又![]() ,即
,即![]() ,∴
,∴![]() .………………2分
.………………2分
∴![]() ,∴
,∴![]() .
.
所以切点为![]() ,代入切线方程得:
,代入切线方程得:![]() ,∴
,∴![]() .………………4分
.………………4分
(II)令![]() ,则
,则![]() 的定义域为
的定义域为![]() .
.
在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 下方等价于
下方等价于![]() 在区间
在区间![]() 上恒成立.
上恒成立.
∵![]() ,………………5分
,………………5分
令![]() ,得
,得![]() 或
或![]() .………………6分
.………………6分
①若![]() ,则
,则![]() .∴在
.∴在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() .
.
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
∴![]() ,
,
∴与![]() 在区间
在区间![]() 上恒成立相背,不符合题意.………………8分
上恒成立相背,不符合题意.………………8分
②若![]() 时,则
时,则![]() ,∵在
,∵在![]() 上有
上有![]() ,∴
,∴![]() 在区间
在区间![]() 递增.
递增.
∴![]() ,∴不符合题意.………………10分
,∴不符合题意.………………10分
③若![]() ,则
,则![]() ,∵在区间
,∵在区间![]() 上有
上有![]() ,则
,则![]() 在区间
在区间![]() 递减.
递减.
∴![]() 在
在![]() 恒成立,要使
恒成立,要使![]() 在
在![]() 恒成立,只需
恒成立,只需![]() .
.
∴![]() ,
,
∴![]() .
.
综上,当![]() 时,函数
时,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方.………………12分
下方.………………12分

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 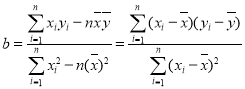 ,
, ![]() .
.