题目内容
圆心在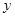 轴上,且与直线
轴上,且与直线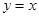 相切于点
相切于点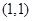 的圆的方程为____________________.
的圆的方程为____________________.
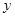 轴上,且与直线
轴上,且与直线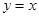 相切于点
相切于点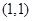 的圆的方程为____________________.
的圆的方程为____________________.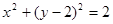
试题分析:设圆心为(0,b),半径为r,则圆的方程为x2+(y-b)2=r2,依题意有
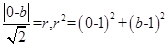 ,
,解得
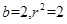 ,所以圆的方程为x2+(y-2)2=2.故答案为:x2+(y-2)2=2。
,所以圆的方程为x2+(y-2)2=2.故答案为:x2+(y-2)2=2。点评:此题主要考查了直线与圆的位置关系。当直线与圆相切时,圆心到直线的距离等于圆的半径,且切线垂直于过切点的半径.

练习册系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 轴交于
轴交于 两点,
两点, 是圆
是圆 且与
且与 ,直线
,直线 交直线
交直线 ,直线
,直线 交直线
交直线 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标. 与圆
与圆 的公共弦所在直线的方程为
的公共弦所在直线的方程为  .
. 和
和 轴相切,圆心在直线
轴相切,圆心在直线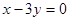 上,且被直线
上,且被直线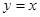 截得的弦长为
截得的弦长为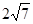
 ,求圆
,求圆 关于
关于 对称的圆的方程是( )
对称的圆的方程是( )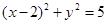



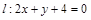 及圆
及圆 的交点,并且有最小面积的圆
的交点,并且有最小面积的圆 的方程为
的方程为 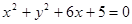 外切,同时与圆
外切,同时与圆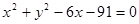 内切,求动圆圆心
内切,求动圆圆心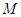 的轨迹方程,并说明它是什么样的曲线。
的轨迹方程,并说明它是什么样的曲线。 外接圆半径
外接圆半径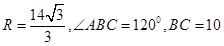 ,弦
,弦 在
在 轴上且
轴上且 轴垂直平分
轴垂直平分 且以
且以 为焦点的椭圆方程
为焦点的椭圆方程