题目内容
(文)(本题满分12分)已知圆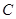 和
和 轴相切,圆心在直线
轴相切,圆心在直线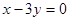 上,且被直线
上,且被直线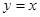 截得的弦长为
截得的弦长为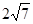
 ,求圆
,求圆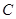 的标准方程。
的标准方程。
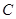 和
和 轴相切,圆心在直线
轴相切,圆心在直线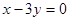 上,且被直线
上,且被直线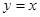 截得的弦长为
截得的弦长为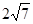
 ,求圆
,求圆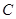 的标准方程。
的标准方程。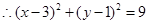 或
或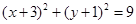
试题分析:(文)解:设所求圆方程为
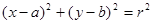 ,
,由圆心在直线
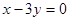 上
上则圆心为
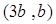 ,半径为
,半径为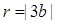 ,
,则
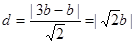 而
而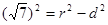 ,则
,则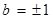
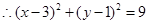 或
或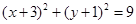
点评:解决该试题的关键是求解圆心坐标和圆的半径。那么要充分利用直线与圆相交时的性质,圆心距和弦长,以及圆的半径的勾股定理来求解,同时注意圆与坐标轴相切意味着圆心的一个坐标确定了。属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
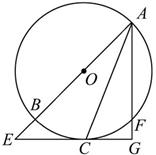
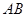 过圆心
过圆心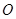 ,交⊙
,交⊙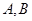 ,直线
,直线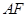 交⊙
交⊙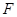 (不与
(不与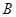 重合),直线
重合),直线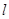 与⊙
与⊙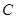 ,交
,交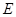 ,且与
,且与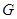 ,连结
,连结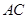 .
.
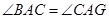 ;
; 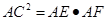 .
.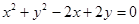 的周长是( )
的周长是( )



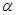 与球O相交于周长为
与球O相交于周长为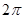 的⊙
的⊙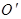 ,A、B为⊙
,A、B为⊙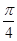 ,且A、B的球面距离为
,且A、B的球面距离为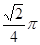 ,则
,则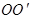 的长度为( )
的长度为( )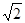 C.
C.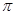 D.2
D.2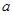 ,
,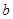 ,
,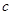 成等差数列且公差不为零,则直线
成等差数列且公差不为零,则直线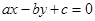 被圆
被圆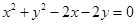 截得的弦长的最小值为_______.
截得的弦长的最小值为_______. 则满足条件的查找的条数是____________。
则满足条件的查找的条数是____________。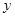 轴上,且与直线
轴上,且与直线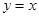 相切于点
相切于点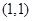 的圆的方程为____________________.
的圆的方程为____________________.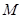 过两点
过两点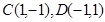 ,且圆心
,且圆心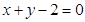 上.
上.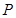 是直线
是直线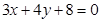 上的动点,
上的动点,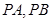 是圆
是圆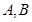 为切点,求四边形
为切点,求四边形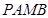 面积的最小值.
面积的最小值.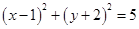 上一点
上一点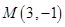 的切线方程是( )
的切线方程是( )


