题目内容
(本小题满分10分)已知一动圆与圆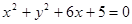 外切,同时与圆
外切,同时与圆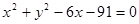 内切,求动圆圆心
内切,求动圆圆心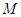 的轨迹方程,并说明它是什么样的曲线。
的轨迹方程,并说明它是什么样的曲线。
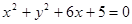 外切,同时与圆
外切,同时与圆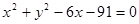 内切,求动圆圆心
内切,求动圆圆心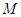 的轨迹方程,并说明它是什么样的曲线。
的轨迹方程,并说明它是什么样的曲线。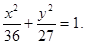 M的轨迹是以
M的轨迹是以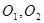 为焦点,长轴长为12的椭圆。
为焦点,长轴长为12的椭圆。试题分析:设动圆圆心为
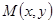 ,半径为R,设已知圆的圆心分别为
,半径为R,设已知圆的圆心分别为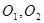 ,将圆方程分别化为标准方程得:
,将圆方程分别化为标准方程得: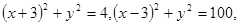 当圆M与圆
当圆M与圆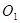 相切时,有
相切时,有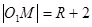 ,同理
,同理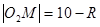 ,得
,得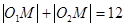 ,所以点M的轨迹是以
,所以点M的轨迹是以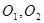 为焦点,长轴长为12的椭圆。其方程为
为焦点,长轴长为12的椭圆。其方程为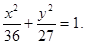
点评:此题主要考查了应用定义法求点的轨迹方程。所谓定义法就是:动点的轨迹符合某种已知几何曲线的定义,可知轨迹方程的形式,再利用待定系数法求出方程的相关系数,这种方法叫做定义法。

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
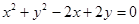 的周长是( )
的周长是( )



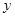 轴上,且与直线
轴上,且与直线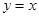 相切于点
相切于点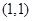 的圆的方程为____________________.
的圆的方程为____________________.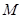 过两点
过两点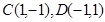 ,且圆心
,且圆心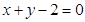 上.
上.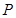 是直线
是直线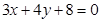 上的动点,
上的动点,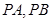 是圆
是圆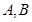 为切点,求四边形
为切点,求四边形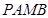 面积的最小值.
面积的最小值.


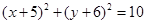
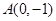 和直线
和直线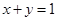 相切,且圆心在直线
相切,且圆心在直线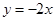 上的圆的方程。
上的圆的方程。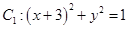 ,圆
,圆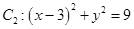 同时外切的动圆圆心的轨迹方程是_____________。
同时外切的动圆圆心的轨迹方程是_____________。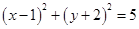 上一点
上一点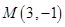 的切线方程是( )
的切线方程是( )



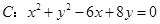 的圆心坐标为( )
的圆心坐标为( )


