题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为
,且以椭圆上的点和长轴两端点为顶点的三角形的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
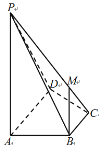
(2)经过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点,且
为一个定点,且![]() (
(![]() 为原点).
为原点).
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据题意得出关于![]() 、
、![]() 、
、![]() 的方程组,解出
的方程组,解出![]() 、
、![]() 的值,进而可求得椭圆
的值,进而可求得椭圆![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,可得点
,可得点![]() ,设点
,设点![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,由
的方程联立,列出韦达定理,由![]() 、
、![]() 、
、![]() 三点共线可得出
三点共线可得出![]()
(1)由题意得 ,解得
,解得![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)由题意知直线![]() 的斜率一定存在,设为
的斜率一定存在,设为![]() ,
,
设![]() 、
、![]() ,则
,则![]() ,设
,设![]() ,
,
联立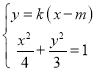 消去
消去![]() 得:
得:![]() ,
,
由![]() 得
得![]() ,即
,即![]() 时,
时,![]() ,
,![]() 一定存在,
一定存在,
![]() ,
,![]() .
.
当斜率![]() 不为
不为![]() 时:因为
时:因为![]() 、
、![]() 、
、![]() 三点共线,
三点共线,![]() ,
,
![]() ,即
,即![]() ,
,
即![]()
化简![]() ,
,
代入韦达定理化简得![]() ,即
,即![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
当斜率![]() 时,直线
时,直线![]() 与
与![]() 轴重合,满足结论.
轴重合,满足结论.
综上,直线![]() 与
与![]() 轴的交点
轴的交点![]() 为一个定点
为一个定点![]() ,且
,且![]()

【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x(![]() )(件)与相应的生产总成本y(万元)的四组对照数据.
)(件)与相应的生产总成本y(万元)的四组对照数据.
x | 5 | 7 | 9 | 11 |
y | 200 | 298 | 431 | 609 |
工厂研究人员建立了y与x的两种回归模型,利用计算机算得近似结果如下:
模型①:![]()
模型②:![]() .
.
其中模型①的残差(实际值-预报值)图如图所示:
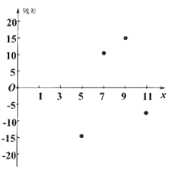
(1)根据残差分析,判断哪一个模型更适宜作为y关于x的回归方程?并说明理由;
(2)市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q(万元)是一个与产量x相关的随机变量,分布列为:
q |
|
|
|
P | 0.5 | 0.4 | 0.1 |
结合你对(1)的判断,当产量x为何值时,月利润的预报期望值最大?最大值是多少(精确到0.1)?