题目内容
【题目】中心在原点的椭圆E的一个焦点与抛物线
的焦点关于直线
对称，且椭圆E与坐标轴的一个交点坐标为
.
（1）求椭圆E的标准方程；
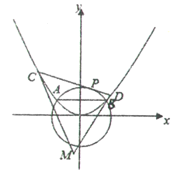
（2）过点
的直线l（直线的斜率k存在且不为0）交E于A，B两点，交x轴于点P点A关于x轴的对称点为D，直线BD交x轴于点Q.试探究
是否为定值？请说明理由.
【答案】（1）
；（2）
为定值4，理由详见解析.
【解析】
（1）椭圆E的右焦点为
，得到
，计算
，得到答案.
（2）设直线l的方程为
，联立方程得到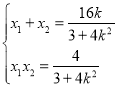
，计算得到
，计算
，得到答案.
（1）因为椭圆E的一个焦点与抛物线
的焦点关于直线
对称，
所以椭圆E的右焦点为，所以.
又椭圆E与坐标轴的一个交点坐标为
，所以，又
，
所以椭圆E的标准方程为.
（2）设直线l的方程为，
，则点
，设
则点
，联立直线l与椭圆E的方程有
，
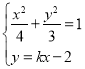得
，所以有
，即
且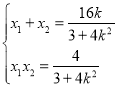，即直线BD的方程为
令\
，得点Q的横坐标为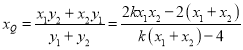
，
代入得：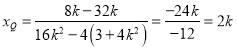
，
所以，所以为定值4.
练习册系列答案
相关题目
