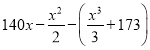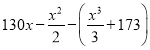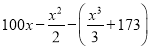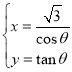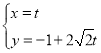题目内容
【题目】2020年是我国全面建成小康社会和“十三五”规划收官之年,也是佛山在经济总量超万亿元新起点上开启发展新征程的重要历史节点.作为制造业城市,佛山一直坚持把创新摆在制造业发展全局的前置位置和核心位置,聚焦打造成为面向全球的国家制造业创新中心,走“世界科技+佛山智造+全球市场”的创新发展之路.在推动制造业高质量发展的大环境下,佛山市某工厂统筹各类资源,进行了积极的改革探索.下表是该工厂每月生产的一种核心产品的产量x（
）（件）与相应的生产总成本y（万元）的四组对照数据.
x | 5 | 7 | 9 | 11 |
y | 200 | 298 | 431 | 609 |
工厂研究人员建立了y与x的两种回归模型,利用计算机算得近似结果如下：
模型①：
模型②：
.
其中模型①的残差（实际值－预报值）图如图所示：
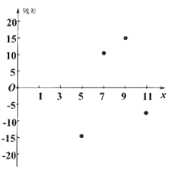
（1）根据残差分析,判断哪一个模型更适宜作为y关于x的回归方程？并说明理由；
（2）市场前景风云变幻,研究人员统计历年的销售数据得到每件产品的销售价格q（万元）是一个与产量x相关的随机变量,分布列为：
q |
|
|
|
P | 0.5 | 0.4 | 0.1 |
结合你对（1）的判断,当产量x为何值时,月利润的预报期望值最大？最大值是多少（精确到0.1）？
【答案】（1）模型①更适宜作为y关于x的回归方程,见解析（2）产量为11件时,月利润的预报期望值最大,最大值是774.8万元.
【解析】
(1)作出模型②的残点图,再对比①的残点图分析即可.
(2)根据题意作出Y的分布列,进而得出其数学期望
,再求导分析其单调性求出最大值即可.
（1）模型②的残差数据如下表：
x | 5 | 7 | 9 | 11 |
y | 200 | 298 | 431 | 609 |
| 20 |
|
| 21 |
模型②的残点图如图所示.
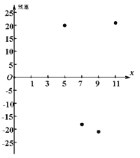
模型①更适宜作为y关于x的回归方程,因为：
理由1：模型①这个4个样本点的残差的绝对值都比模型②的小.
理由2：模型①这4个样本的残差点落在的带状区域比模型②的带状区域更窄.
理由3：模型①这4个样本的残差点比模型②的残差点更贴近x轴.
（2）设月利润为Y,由题意知
,则Y的分布列为：
Y |
|
|
|
P | 0.5 | 0.4 | 0.1 |
.
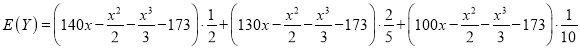
设函数
,
,
,
令
,解得
或
（舍）,
当
时,
,则
单调递增；当
时,
,则单调递减.
则函数的最大值
,即产量为11件时,月利润的预报期望值最大,最大值是774.8万元.
