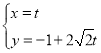题目内容
【题目】在正三棱锥P﹣ABC中，PA，PB，PC两两垂直，
，点E在线段AB上，且AE＝2EB，过点E作该正三棱锥外接球的截面，则所得截面圆面积的最小值是（ ）
A.
B.
C.
D.
【答案】A
【解析】
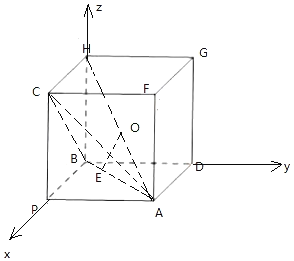
构造以PA，PB，PC为棱长的正方体PADB﹣CFGH，且该正方体棱长为
，以B为原点，BP为x轴，BD为y轴，BH为z轴，建立空间直角坐标系，则该正三棱锥外接球球心为AH中点O，半径为R
，求出EO
，当所得截面圆面积取最小值时截面圆的圆心为E，从而当所得截面圆面积取最小值时截面圆的半径为r
，由此能求出所得截面圆面积的最小值.
∵在正三棱锥P﹣ABC中，PA，PB，PC两两垂直，
，
∴构造以PA，PB，PC为棱长的正方体PADB﹣CFGH，且该正方体棱长为，
以B为原点，BP为x轴，BD为y轴，BH为z轴，建立空间直角坐标系，
则该正三棱锥外接球球心为AH中点O，半径为R，
∵点E在线段AB上，且AE＝2EB，
∴E（
，，0），O（
），
EO
，
过点E作该正三棱锥外接球的截面，当所得截面圆面积取最小值时截面圆的圆心为E，
∴当所得截面圆面积取最小值时截面圆的半径为：
r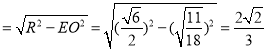
，
∴过点E作该正三棱锥外接球的截面，
则所得截面圆面积的最小值为S＝πr2
.
故选：A.
练习册系列答案
相关题目
