题目内容
已知数列{an}满足an+2=an+1+an,若a1=1,a5=8,则a3=( )
| A.1 | B.2 | C.3 | D.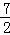 |
C
由an+2=an+1+an,得an+3=an+2+an+1=2an+1+an,
即当n=2时a5=2a3+a2,
当n=1时,a3=a2+a1,即a2=a3﹣a1,
两式联立得a5=2a3+a2=2a3+a3﹣a1,
∵a1=1,a5=8,
∴8=3a3﹣1,
即a3=3,
故选:C
即当n=2时a5=2a3+a2,
当n=1时,a3=a2+a1,即a2=a3﹣a1,
两式联立得a5=2a3+a2=2a3+a3﹣a1,
∵a1=1,a5=8,
∴8=3a3﹣1,
即a3=3,
故选:C

练习册系列答案
相关题目

 ,数列{bn}的前n项和为Tn.证明:对于任意n
,数列{bn}的前n项和为Tn.证明:对于任意n  N*,都有Tn<
N*,都有Tn<
 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
) 的值;
的值; +
+ +…+
+…+ <
< .
. 是首项为1,公比为
是首项为1,公比为 的等比数列,若
的等比数列,若 是等差数列,则
是等差数列,则 ( )
( )



 的公差
的公差 大于0,
大于0, 是方程
是方程 的两根.
的两根.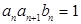 ,求数列
,求数列 的前
的前 项和.
项和.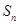 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且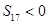 ,则当
,则当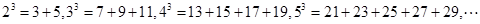 ,若类似上面各式方法将
,若类似上面各式方法将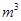 分拆得到的等式右边最后一个数是
分拆得到的等式右边最后一个数是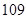 ,则正整数
,则正整数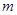 等于____.
等于____.