题目内容
设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
)
(1) 求 的值;
的值;
(2) 求数列 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 +
+ +…+
+…+ <
< .
.
 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
)(1) 求
 的值;
的值;(2) 求数列
 的通项公式;
的通项公式;(3) 证明:对一切正整数
 ,有
,有 +
+ +…+
+…+ <
< .
.(1) 4
(2) n2
(3)见解析
(2) n2
(3)见解析
(1) 依题意,2S1=a2- -1-
-1- ,又
,又 ,所以
,所以 ;
;
(2) 当 时, 2Sn=nan+1-
时, 2Sn=nan+1- n3-n2-
n3-n2- n,
n,
∴2Sn-1=(n-1)an- (n-1)3-(n-1)2-
(n-1)3-(n-1)2- (n-1),
(n-1),
两式相减得2an=nan+1-(n-1)an- (3n2-3n+1)-(2n-1)-
(3n2-3n+1)-(2n-1)-
整理得 ,即
,即 -
- =1,
=1,
又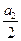 -
- =1, 故数列{
=1, 故数列{ }是首项为
}是首项为 =1,公差为
=1,公差为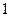 的等差数列,
的等差数列,
所以 =1+(n-1)×1=n,所以
=1+(n-1)×1=n,所以 .
.
(3) 当 时,
时,  =1<
=1< ;
;
当 时,
时,  +
+ =1+
=1+ =
= <
< ;
;
当 时,
时,  =
= <
< =
= -
- ,此时
,此时
 +
+ +…+
+…+ =1+
=1+ +
+ +…+
+…+ <1+
<1+ +(
+( -
- )+(
)+( -
- )+…+(
)+…+( -
- )
)
=1+ +
+ -
- =
= -
- <
<
综上,对一切正整数 ,有
,有 +
+ +…+
+…+ <
< .
.
 -1-
-1- ,又
,又 ,所以
,所以 ;
;(2) 当
 时, 2Sn=nan+1-
时, 2Sn=nan+1- n3-n2-
n3-n2- n,
n,∴2Sn-1=(n-1)an-
 (n-1)3-(n-1)2-
(n-1)3-(n-1)2- (n-1),
(n-1),两式相减得2an=nan+1-(n-1)an-
 (3n2-3n+1)-(2n-1)-
(3n2-3n+1)-(2n-1)-
整理得
 ,即
,即 -
- =1,
=1,又
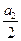 -
- =1, 故数列{
=1, 故数列{ }是首项为
}是首项为 =1,公差为
=1,公差为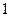 的等差数列,
的等差数列,所以
 =1+(n-1)×1=n,所以
=1+(n-1)×1=n,所以 .
.(3) 当
 时,
时,  =1<
=1< ;
;当
 时,
时,  +
+ =1+
=1+ =
= <
< ;
;当
 时,
时,  =
= <
< =
= -
- ,此时
,此时 +
+ +…+
+…+ =1+
=1+ +
+ +…+
+…+ <1+
<1+ +(
+( -
- )+(
)+( -
- )+…+(
)+…+( -
- )
)=1+
 +
+ -
- =
= -
- <
<
综上,对一切正整数
 ,有
,有 +
+ +…+
+…+ <
< .
.
练习册系列答案
相关题目
 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。 ,求数列
,求数列 的最大项的值与最小项的值。
的最大项的值与最小项的值。 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: ;
; 为数表中第
为数表中第 行的第
行的第 个数.
个数. 和
和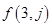 ;
; 关于
关于 )的表达式.
)的表达式.
 满足
满足 (
( ).
).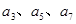 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,数列
,数列
 的前
的前 ,求
,求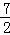
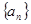 是等差数列,且
是等差数列,且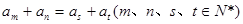 ,
,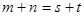 ;
; 是等差数列
是等差数列 项的和,则
项的和,则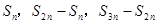 成等差数列;
成等差数列;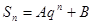 ;(其中
;(其中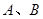 是非零常数,
是非零常数,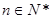 ),则
),则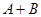 为零.
为零. }满足
}满足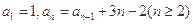 ,则
,则 的通项公式为( )
的通项公式为( )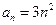



 中,
中, 的值是
的值是