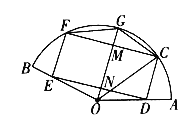
题目内容
【题目】在![]() (n≥2)个实数组成的n行n列的数表中,
(n≥2)个实数组成的n行n列的数表中, ![]() 表示第i行第j列的数,记
表示第i行第j列的数,记![]() .
. ![]() 若
若![]() {-1,0,1} (
{-1,0,1} (![]() ),且r1,r2,…,rn,c1,c2,..,cn,两两不等,则称此表为“n阶H表”,记
),且r1,r2,…,rn,c1,c2,..,cn,两两不等,则称此表为“n阶H表”,记
H={ r1,r2,…,rn,c1,c2,..,cn}.
(I)请写出一个“2阶H表”;
(II)对任意一个“n阶H表”,若整数![]() ,且
,且![]() ,求证:
,求证: ![]() 为偶数;
为偶数;
(Ⅲ)求证:不存在“5阶H表”.
【答案】(I)见解析;(II)见解析;(III)见解析.
【解析】试题分析:(I)由单一即可写出;
(II)对任意一个“![]() 阶
阶![]() 表”,
表”, ![]() 表示第
表示第![]() 行所有数的和,
行所有数的和, ![]() 表示第
表示第![]() 列所有数的和
列所有数的和
(![]() ),可知
),可知![]()
![]() . 进而得到
. 进而得到![]()
![]()
![]()
![]() .所以
.所以![]()
![]() 为偶数.
为偶数.
(III)假设存在一个“![]() 阶
阶![]() 表”,则由(II)知
表”,则由(II)知![]() ,且
,且![]() 和
和![]() 至少有一个成立,不妨设
至少有一个成立,不妨设![]() .
.
设![]() ,则
,则![]() ,于是
,于是![]() ,因而可设
,因而可设![]() ,
,
![]() ,
, ![]() .
.
分①若 3是某列的和,②若3是某行的和,讨论均可得出矛盾,综上,不存在“5阶![]() 表”.
表”.
试题解析:
(I)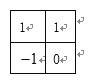 ;
;
(II)对任意一个“![]() 阶
阶![]() 表”,
表”, ![]() 表示第
表示第![]() 行所有数的和,
行所有数的和, ![]() 表示第
表示第![]() 列所有数的和
列所有数的和
(![]() ).
). ![]() 与
与![]() 均表示数表中所有数的和,所以
均表示数表中所有数的和,所以![]()
![]() .
.
因为![]() ,所以
,所以![]() 只能取
只能取![]() 内的整数.
内的整数.
又因为![]() 互不相等,
互不相等, ![]() 且
且![]() ,
,
所以![]() ,
,
所以![]()
![]()
![]()
![]() .
.
所以![]()
![]() 为偶数.
为偶数.
(III)假设存在一个“![]() 阶
阶![]() 表”,则由(II)知
表”,则由(II)知![]() ,且
,且![]() 和
和![]() 至少有一个成立,不妨设
至少有一个成立,不妨设![]() .
.
设![]() ,则
,则![]() ,于是
,于是![]() ,因而可设
,因而可设![]() ,
,
![]() ,
, ![]() .
.
①若 3是某列的和,由于![]() ,故只能是前四列某列的和,不妨设是第一列,即
,故只能是前四列某列的和,不妨设是第一列,即![]() .现考虑
.现考虑![]() ,只能是
,只能是![]() 或
或![]() ,不妨设
,不妨设![]() ,即
,即![]() ,由
,由![]() 两两不等知
两两不等知![]() 两两不等,不妨设
两两不等,不妨设![]() ,若
,若![]() 则
则![]() ;若
;若![]() 则
则![]() ;若
;若![]() 则
则![]() ,均与已知矛盾.
,均与已知矛盾.
②若3是某行的和,不妨设![]() ,则第4行至少有3个1,若这3个1是前四个中某三个数,不妨设
,则第4行至少有3个1,若这3个1是前四个中某三个数,不妨设![]() ,则第五行前三个数只能是3个不同的数,不妨设
,则第五行前三个数只能是3个不同的数,不妨设
![]() ,则
,则![]() 矛盾,故第四行只能前四个数有2个1,第五个数为1,不妨设
矛盾,故第四行只能前四个数有2个1,第五个数为1,不妨设![]() ,所以
,所以![]() ,第五行只能是2个0,3个
,第五行只能是2个0,3个![]() 或1个1,4个
或1个1,4个![]() .则
.则![]() 至少有两个数相同,不妨设
至少有两个数相同,不妨设![]() ,则
,则![]() 与已知矛盾.
与已知矛盾.
综上,不存在“5阶![]() 表”.
表”.

 应用题作业本系列答案
应用题作业本系列答案【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
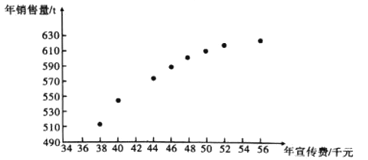
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
![]() 根据散点图判断,
根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
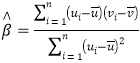 ,
,![]() .
.