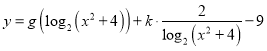��Ŀ����
����Ŀ����ͼ,ijС��Ϊ��������,����������,�ƻ���һ��뾶ΪR��RΪ������������������,�������εĻ�̳CDEF��һ�������ε�ˮ��FCG.����![]() ,OΪԲ��,
,OΪԲ��,![]() ,C,G,F������Բ����,D,E�ֱ��ڰ뾶OA,OB��,��OG��CF,DE�ֱ���M,N,
,C,G,F������Բ����,D,E�ֱ��ڰ뾶OA,OB��,��OG��CF,DE�ֱ���M,N,![]() .
.
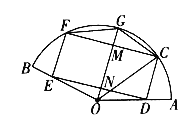
��1�����FCG�����S����![]() �Ĺ�ϵʽ,��д��������
�Ĺ�ϵʽ,��д��������
��2����R=10��,��̳ÿƽ���������300Ԫ,���ʾ��λ�̳���������Ƕ��٣���ȡ![]() ��
��
���𰸡�(1) ![]() . (2)17320Ԫ
. (2)17320Ԫ
��������
��1������Բ�ļ�������֤��![]() ������
������![]() ��ʾ��
��ʾ��![]() ���ɴ����������
���ɴ����������![]() ����ı���ʽ�������
����ı���ʽ�������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2�����![]() ���ɴ���þ���
���ɴ���þ���![]() ����ı���ʽ�����ø����ǹ�ʽ��������Ǻ�������ֵ�ķ�������þ���
����ı���ʽ�����ø����ǹ�ʽ��������Ǻ�������ֵ�ķ�������þ���![]() ��������ֵ���Ӷ����������.
��������ֵ���Ӷ����������.
��1������OF,��Ϊ![]() ,����
,����![]() ,��
,��![]() ,����
,����![]() .
.
��Ϊ![]() ,����
,����![]() ,����
,����![]() ,
,![]() ,
,
����![]() .
.
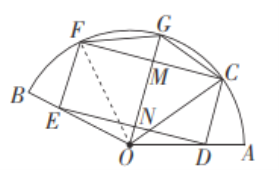
��2����Ϊ![]() ,
,
����![]() ,
,
����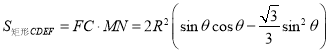
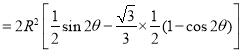
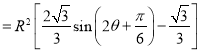 .
.
��Ϊ![]() ,���Ե�
,���Ե�![]() ʱ,
ʱ,![]() ���.
���.
�ʾ��λ�̳����������![]() Ԫ.
Ԫ.

����Ŀ�������ź�����Ѿ���Ϊ�й����ջ��ȴ���ʱ�dz�ϲ����һ����С���ռ�����20��ͬѧ���괺���ڼ�����������![]() ��Ԫ�����£���������ȡ��������
��Ԫ�����£���������ȡ��������
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
����20�����ݽ��з��飬�����Ƶ�����£�
��� | ��������� | Ƶ�� |
|
| 2 |
|
| 9 |
|
|
|
|
| 3 |
|
|
|
������д����ֵ�����ش���20��ͬѧ�����ĺ��������λ�������ĸ����
��������![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ���Էֱ�Ƚ�
���Էֱ�Ƚ�![]() ��
��![]() ��
��![]() ��
��![]() �Ĵ�С����ֻ��д�����ۣ�
�Ĵ�С����ֻ��д�����ۣ�
��������![]() �����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ
�����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������