题目内容
【题目】有下列说法
①互斥事件不一定是对立事件，对立事件一定是互斥事件
②演绎推理是从特殊到一般的推理，它的一般模式是“三段论”
③残差图的带状区域的宽度越窄，说明模型拟合精度越高，回归方程的预报精度越高
④若
，则事件
与
互斥且对立
⑤甲乙两艘轮船都要在某个泊位停靠4小时，假定它们在一昼夜的时间段中随机到达，则这两艘船中至少有一艘在停靠泊位时必须等待的概率为
．
其中正确的说法是______（写出全部正确说法的序号）．
【答案】①③⑤
【解析】
由事件的互斥和对立的概念可判断①；由演绎推理的定义可判断②；由残差图的形状可判断③；考虑几何概型事件的概率可判断④；设出甲、乙到达的时刻，列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件，利用线性规划作出平面区域，利用几何概型概率公式求出概率，可判断⑤．
对于①，互斥事件不一定是对立事件，但对立事件一定是互斥事件，故①正确；
对于②，演绎推理是从一般到特殊的推理，它的一般模式是“三段论”，故②错误；
对于③，残差图的带状区域的宽度越窄，说明模型拟合精度越高，回归方程的预报精度越高，故③正确；
对于④，若P（A∪B）=P（A）+P（B）=1，则事件A与B不一定互斥且对立，
例如几何概型：在[-1,1]任取实数
，则事件A；
事件B：
则有P（A∪B）=P（A）+P（B）=1，但事件A与B不互斥，故④错误；
对于⑤，设甲到达的时刻为x，乙到达的时刻为y则所有的基本事件构成的
区域Ω满足
，
这两艘船中至少有一艘在停靠泊位时必须等待包含的基本事件构成的区域A满足
，作出对应的平面区域如图，
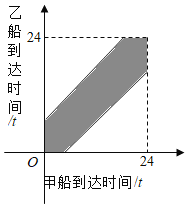
这两艘船中至少有一艘在停靠泊位时必须等待的概率
，故⑤正确．
故答案为：①③⑤．
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动．小明收集班内20名同学今年春节期间抢到红包金额
（元）如下（四舍五入取整数）：
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组，各组的频数如下：
组别 | 红包金额分组 | 频数 |
|
| 2 |
|
| 9 |
|
|
|
|
| 3 |
|
|
|
（Ⅰ）写出的值，并回答这20名同学抢到的红包金额的中位数落在哪个组别；
（Ⅱ）记
组红包金额的平均数与方差分别为
组红包金额的平均数与方差分别为
，试分别比较
与
、
与
的大小；（只需写出结论）
（Ⅲ）从
两组的所有数据中任取2个数据，记这2个数据差的绝对值为
，求
的分布列和数学期望．
