Question

【题目】已知椭圆=1（a＞b＞0）的右焦点为F（2，0），且过点（2，）．

（1）求椭圆的标准方程；

（2）设直线l：y=kx（k＞0）与椭圆在第一象限的交点为M，过点F且斜率为-1的直线与l交于点N，若sin∠FON（O为坐标原点），求k的值．

Answer 1

【答案】（1）；（2）或

【解析】

（1）根据题意列出有关a2、b2的方程组，求出这两个数的值，即可求出椭圆的标准方程；（2）设点M的坐标为（x1，y1），点N的坐标（x2，y2），利用已知条件sin∠FON，得出，然后将直线l的方程分别与椭圆方程和直线NF的方程联立，求出点M、N的坐标，结合条件可求出k的值．

（1）由题意可知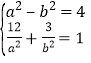，解得a2＝16，b2＝12（负值舍去），

所以椭圆方程为；

（2）设点M的坐标为，点N的坐标，

由题可知，故，

因为，而，所以，

由，可得，

所以，

由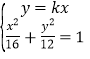，消去x，可得，

易知直线NF的方程为，

由，消去x，可得，

所以，整理得52k2﹣96k+27＝0，

解得或．