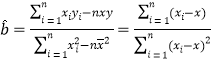题目内容
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据![]() ,
,![]() ,得到
,得到![]() ,列式求值即可.
,列式求值即可.
(2)![]() 坐标化可得
坐标化可得![]() ,原点
,原点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() ②,将①式代入②式得:
②,将①式代入②式得:![]() ,得解.
,得解.
(1)![]() ,
,![]() ,
,
![]() ,
,
则![]() ,化简得
,化简得![]() ,
,
又![]() ,
,![]() ,
,
则![]() ,得
,得![]() ,则
,则![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意知,直线![]() 不过原点,设
不过原点,设![]() ,
,![]() ,
,
(i)当直线![]() 轴时,直线
轴时,直线![]() 的方程为
的方程为![]() 且
且![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
解得![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,
,
![]() 原点
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(ii)当直线![]() 不垂直于
不垂直于![]() 轴时,
轴时,
设直线![]() 的方程为
的方程为![]() ,联立直线和椭圆方程消去
,联立直线和椭圆方程消去![]() 得
得![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() .
.
![]() ,
,![]() ,故
,故![]() ,
,
即![]() ,
,![]() ①,
①,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则![]()
![]() ②,将①式代入②式得:
②,将①式代入②式得:![]() ,
,
![]() .
.
综上,点![]() 到直线
到直线![]() 的距离为定值
的距离为定值![]() .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】某人对东北一种松树的生长进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据,选择h=mt+b与h=loga(t+1)来刻画h与t的关系,你认为哪个符合?并预测第8年的松树高度.
t(年) | 1 | 2 | 3 | 4 | 5 | 6 |
h(米) | 0.6 | 1 | 1.3 | 1.5 | 1.6 | 1.7 |
【题目】某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
频数 | 35 | 20 | 25 | 20 |
支持脱欧的人数 | 10 | 10 | 15 | 15 |
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持“脱欧”人数 | |||
不支持“脱欧”人数 | |||
合计 |
附:![]()

(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.