Question

【题目】某人对东北一种松树的生长进行了研究，收集了其高度h(米)与生长时间t(年)的相关数据，选择h＝mt＋b与h＝loga(t＋1)来刻画h与t的关系，你认为哪个符合？并预测第8年的松树高度．

t(年)	1	2	3	4	5	6
h(米)	0.6	1	1.3	1.5	1.6	1.7

Answer 1

【答案】2米

【解析】试题分析：根据表格年份与高度数据画出散点图，由散点图的分布规律与特征来选择合适函数。由散点图，显然选择对数函数模型更合适。代入一个点（一般尽量选中间点，不取两端的）求得参数，得到拟合函数，代入t=8,即可估测8年松树的高度。

试题分析：据表中数据作出散点图如图：

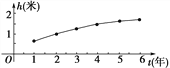
由图可以看出用一次函数模型不吻合，选用对数型函数比较合理．

将(2,1)代入到h＝loga(t＋1)中，得1＝loga3，解得a＝3.即h＝log3(t＋1)．

当t＝8时，h＝log3(8＋1)＝2，

故可预测第8年松树的高度为2米．