题目内容
8．设数列{an}的前n项和为Sn，若Sn+an=n．求证：数列{an-1}是等比数列．分析 通过Sn+an=n与Sn+1+an+1=n+1作差、整理得2an+1-an=1，变形可知an+1-1=$\frac{1}{2}$（an-1），进而可知数列{an-1}是以-$\frac{1}{2}$为首项、$\frac{1}{2}$为公比的等比数列．
解答 证明：∵Sn+an=n，
∴Sn+1+an+1=n+1，
两式相减得：2an+1-an=1，
整理得：an+1-1=$\frac{1}{2}$（an-1），
又∵a1+a1=1，即a1=$\frac{1}{2}$，
∴a1-1=$\frac{1}{2}$-1=-$\frac{1}{2}$，
∴数列{an-1}是以-$\frac{1}{2}$为首项、$\frac{1}{2}$为公比的等比数列．
点评 本题考查等比数列的判定，注意解题方法的积累，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
13．
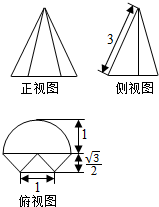一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）
一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）| A． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |