题目内容
20.已知(2x+$\frac{1}{\sqrt{x}}$)n的二项式系数和等于64.(1)求n的值及展开式中各项的系数和;
(2)展开式中是否存在二次项?如果存在,请求出该二次项,如果不存在?请说明理由.
分析 (1)根据二项式系数和求出n的值,再令x=1求出展开式中各项的系数和;
(2)利用展开式中的通项公式,求出r的值,判断是否符合题意即可.
解答 解:(1)∵(2x+$\frac{1}{\sqrt{x}}$)n的二项式系数和等于64,
∴2n=64,解得n=6;
∴令x=1,得展开式中各项的系数和为(2+1)6=36;
(2)${(2x+\frac{1}{\sqrt{x}})}^{6}$展开式中,通项为
Tr+1=${C}_{6}^{r}$•(2x)6-r•${(\frac{1}{\sqrt{x}})}^{r}$=${C}_{6}^{r}$•26-r•${x}^{6-\frac{3r}{2}}$,
令6-$\frac{3r}{2}$=2,
解得r=$\frac{8}{3}$,不合题意,
所以展开式中不存在x的二次项.
点评 本题考查了二项式定理的灵活应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.设M和P是两个非空集合,定义M与P的差集为M-P={x|x∈M,且x∉P},则M-(M-P)=( )
| A. | P | B. | M∩P | C. | M∪P | D. | M |
11.执行如图所示的程序框图,若输出b=3,则输入的实数a的取值范围是( )
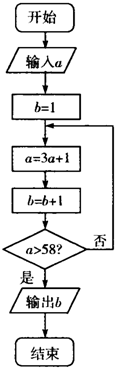

| A. | (19,+∞) | B. | (8,19] | C. | (6,19] | D. | ($\frac{5}{3}$,6] |
12.在△ABC中,b=3,c=8$\sqrt{3}$,∠A=$\frac{π}{6}$,则S△ABC=( )
| A. | 12$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 36 | D. | 18 |
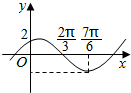 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.