题目内容
(本小题满分12分)设数列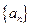 的前
的前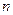 项和为
项和为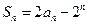 ,
,
(Ⅰ)求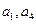 (Ⅱ)证明:
(Ⅱ)证明: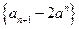 是等比数列;(Ⅲ)求
是等比数列;(Ⅲ)求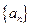 的通项公式
的通项公式
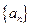 的前
的前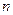 项和为
项和为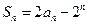 ,
,(Ⅰ)求
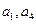 (Ⅱ)证明:
(Ⅱ)证明: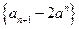 是等比数列;(Ⅲ)求
是等比数列;(Ⅲ)求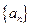 的通项公式
的通项公式(Ⅰ)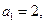
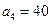 (Ⅲ)
(Ⅲ)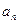
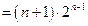
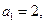
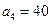 (Ⅲ)
(Ⅲ)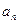
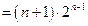
(Ⅰ)因为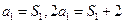 ,所以
,所以
由 知
知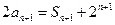

得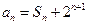 ①所以
①所以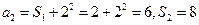
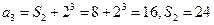
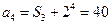
(Ⅱ)由题设和①式知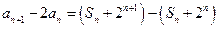
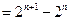
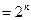
所以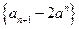 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。
(Ⅲ)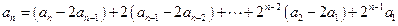
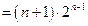
【点评】:此题重点考察数列的递推公式,利用递推公式求数列的特定项,通项公式等;
【突破】:推移脚标两式相减是解决含有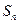 的递推公式的重要手段,使其转化为不含
的递推公式的重要手段,使其转化为不含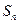 的递推公式,从而针对性的解决;在由递推公式求通项公式时应重视首项是否可以被吸收是易错点,同时注意利用题目设问的层层深入,前一问常为解决后一问的关键环节为求解下一问指明方向。
的递推公式,从而针对性的解决;在由递推公式求通项公式时应重视首项是否可以被吸收是易错点,同时注意利用题目设问的层层深入,前一问常为解决后一问的关键环节为求解下一问指明方向。
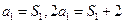 ,所以
,所以
由
 知
知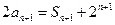

得
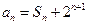 ①所以
①所以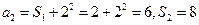
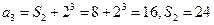
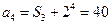
(Ⅱ)由题设和①式知
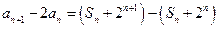
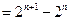
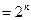
所以
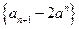 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。(Ⅲ)
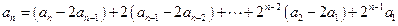
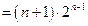
【点评】:此题重点考察数列的递推公式,利用递推公式求数列的特定项,通项公式等;
【突破】:推移脚标两式相减是解决含有
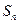 的递推公式的重要手段,使其转化为不含
的递推公式的重要手段,使其转化为不含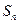 的递推公式,从而针对性的解决;在由递推公式求通项公式时应重视首项是否可以被吸收是易错点,同时注意利用题目设问的层层深入,前一问常为解决后一问的关键环节为求解下一问指明方向。
的递推公式,从而针对性的解决;在由递推公式求通项公式时应重视首项是否可以被吸收是易错点,同时注意利用题目设问的层层深入,前一问常为解决后一问的关键环节为求解下一问指明方向。
练习册系列答案
相关题目
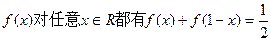 (I)求
(I)求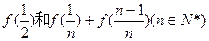 的值;(II)数列{an}满足
的值;(II)数列{an}满足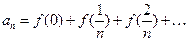
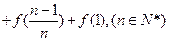 数列{an}是等差数列吗?请给予证明;
数列{an}是等差数列吗?请给予证明;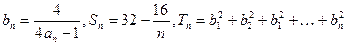 ,试比较Tn与Sn的大小.
,试比较Tn与Sn的大小.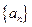 中,
中,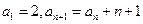 ,则通项
,则通项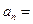 ___________。
___________。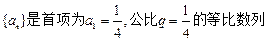 ,设
,设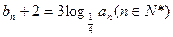 ,数列
,数列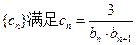 .(Ⅰ)求数列
.(Ⅰ)求数列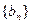 的通项公式;(Ⅱ)若数列
的通项公式;(Ⅱ)若数列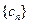 的前
的前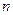 项和为
项和为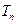 ,求
,求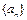 中,
中,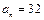 ,
,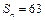 ,
,
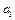 ;
;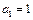 为首项的等比数列,求数列
为首项的等比数列,求数列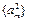 的前m项和
的前m项和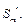
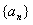 中,
中,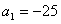 ,前n项和为Sn,S3=S8,则Sn的最小值为( )
,前n项和为Sn,S3=S8,则Sn的最小值为( )




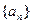 中,
中,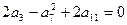 ,数列
,数列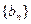 是等比数列,且
是等比数列,且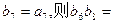 ( )
( )