题目内容
已知中心在原点、焦点在x轴的椭圆的离心率为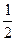 ,且过点(
,且过点(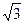 ,
,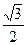 ).
).
(Ⅰ)求椭圆E的方程;
(Ⅱ)若A,B是椭圆E的左、右顶点,直线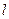 :
: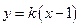 (
(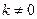 )与椭圆E交于
)与椭圆E交于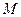 、
、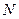 两点,证明直线
两点,证明直线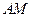 与直线
与直线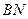 的交点在垂直于
的交点在垂直于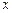 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.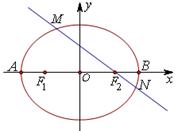
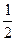 ,且过点(
,且过点(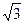 ,
,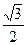 ).
). (Ⅰ)求椭圆E的方程;
(Ⅱ)若A,B是椭圆E的左、右顶点,直线
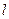 :
: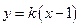 (
(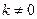 )与椭圆E交于
)与椭圆E交于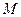 、
、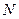 两点,证明直线
两点,证明直线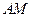 与直线
与直线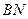 的交点在垂直于
的交点在垂直于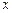 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.
(Ⅰ)
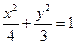 (Ⅱ)直线
(Ⅱ)直线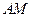 与直线
与直线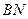 的交点在定直线
的交点在定直线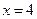 上
上(Ⅰ)依题意,设椭圆
 的方程为
的方程为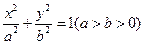 ,
,由已知
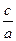 =
=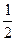 . ①
. ① ∵点(
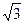 ,
,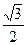 )在椭圆E上,∴
)在椭圆E上,∴ +
+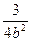 =1. ②
=1. ② 由①、②及
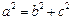 解得,
解得, ,
, .
.∴椭圆
 的方程为
的方程为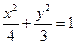 . ……6分
. ……6分(Ⅱ)将直线
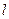 :
: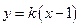 ,代入椭圆方程
,代入椭圆方程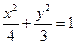 并整理,得
并整理,得 ,
, 设直线
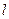 与椭圆
与椭圆 的交点
的交点 ,
, ,
,由根与系数的关系,得
 ,
,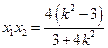 . ……9分
. ……9分 消去
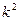 得,
得,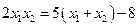 .
. 直线
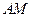 的方程为:
的方程为: ,即
,即 .
.直线
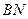 的方程为:
的方程为: ,即
,即 . ……12分
. ……12分由直线
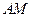 与直线
与直线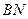 的方程消去
的方程消去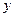 得,
得, .
.∴直线
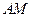 与直线
与直线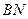 的交点在定直线
的交点在定直线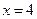 上. ……14分
上. ……14分
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.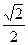 ,则
,则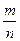 的值是________________________.
的值是________________________. +
+ =1的左、右焦点,点P在椭圆上,△POF2是面积为
=1的左、右焦点,点P在椭圆上,△POF2是面积为 的正三角形,则b2的值为( )
的正三角形,则b2的值为( )

 +
+ =1的长轴长为_________,短轴长为_________,焦点坐标为_________,顶点坐标为_________,离心率为__________.
=1的长轴长为_________,短轴长为_________,焦点坐标为_________,顶点坐标为_________,离心率为__________. ,
,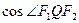 的取值范围;
的取值范围; ,试求直线PM的斜率
,试求直线PM的斜率 的范围。
的范围。



 到两点
到两点 ,写出椭圆
,写出椭圆 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点
的中点 的轨迹方程;
的轨迹方程; 是椭圆
是椭圆 与椭圆相交于
与椭圆相交于 ,
, 两点,当直线
两点,当直线 ,
, 的斜率都存在,并记为
的斜率都存在,并记为 ,
, ,试探究
,试探究 的值是否与点
的值是否与点 上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )




 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值