题目内容
设椭圆 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
(1)求直线l和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上.
 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.(1)求直线l和椭圆的方程;
(2)求证:点F1(-2,0)在以线段AB为直径的圆上.
(1)椭圆方程为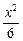 +
+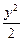 =1.
=1.
 (2)见解析
(2)见解析
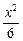 +
+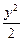 =1.
=1. (2)见解析
(2)见解析可知直线l:y=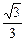 (x+3).
(x+3).
由c=2及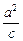 =3,解得a2=6,
=3,解得a2=6,
∴b2=6-22=2.∴椭圆方程为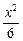 +
+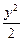 =1.
=1.
 (2)证明:联立方程组
(2)证明:联立方程组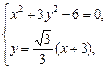
将②代入①,整理得2x2+6x+3=0.
设A(x1,y1)、B(x2,y2),则x1+x2=-3,x1x2=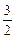 .
.
方法一:k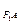 ·k
·k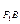 =
=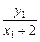 ·
·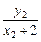 =
=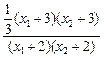
=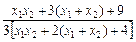 =
=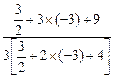 =-1,
=-1,
∴F1A⊥F1B,即∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
方法二: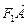 ·
·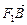 =(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=x1x2+2(x1+x2)+4+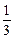 [x1x2+3(x1+x2)+9]
[x1x2+3(x1+x2)+9]
=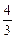 x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,
∴F1A⊥F1B,则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
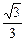 (x+3).
(x+3).由c=2及
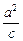 =3,解得a2=6,
=3,解得a2=6,∴b2=6-22=2.∴椭圆方程为
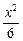 +
+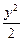 =1.
=1. (2)证明:联立方程组
(2)证明:联立方程组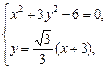
将②代入①,整理得2x2+6x+3=0.
设A(x1,y1)、B(x2,y2),则x1+x2=-3,x1x2=
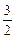 .
.方法一:k
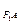 ·k
·k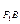 =
=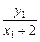 ·
·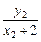 =
=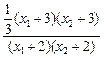
=
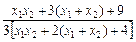 =
=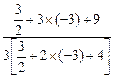 =-1,
=-1,∴F1A⊥F1B,即∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.
方法二:
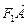 ·
·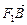 =(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2
=(x1+2,y1)·(x2+2,y2)=(x1+2)(x2+2)+y1y2=x1x2+2(x1+x2)+4+
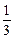 [x1x2+3(x1+x2)+9]
[x1x2+3(x1+x2)+9]=
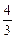 x1x2+3(x1+x2)+7=0,
x1x2+3(x1+x2)+7=0,∴F1A⊥F1B,则∠AF1B=90°.
∴点F1(-2,0)在以线段AB为直径的圆上.

练习册系列答案
相关题目
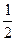 ,且过点(
,且过点(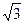 ,
,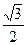 ).
). 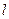 :
: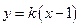 (
(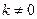 )与椭圆E交于
)与椭圆E交于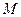 、
、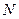 两点,证明直线
两点,证明直线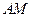 与直线
与直线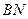 的交点在垂直于
的交点在垂直于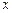 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.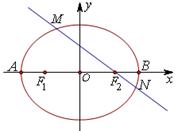
 绕其左焦点逆时针方向旋转90°后所得椭圆方程是
绕其左焦点逆时针方向旋转90°后所得椭圆方程是  ,0),则椭圆的标准方程为_________.
,0),则椭圆的标准方程为_________.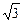 ,求椭圆方程.
,求椭圆方程.
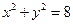 上的每一点的纵坐标压缩到原来的
上的每一点的纵坐标压缩到原来的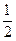 ,对应的横坐标不变,得到曲线C;设
,对应的横坐标不变,得到曲线C;设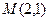 ,平行于OM的直线
,平行于OM的直线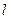 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线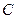 的方程;
的方程; 内一点M(2,0) 引椭圆的动弦AB, 则弦AB的中点N的轨迹方程是 .
内一点M(2,0) 引椭圆的动弦AB, 则弦AB的中点N的轨迹方程是 .  过点(-2,
过点(-2, ),则其焦距为( )
),则其焦距为( )