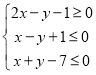题目内容
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)实验开始后,每天的试验费用构成公差为![]() ,首项为
,首项为![]() 的等差数列,通过等差数列的求和公式计算出这
的等差数列,通过等差数列的求和公式计算出这![]() 天所投入的试验费用,然后便可求出
天所投入的试验费用,然后便可求出![]() 的值,再利用等差数列的求和公式求出
的值,再利用等差数列的求和公式求出![]() 天内总计的试验费用,然后再求出每天的平均试验费用,利用基本不等式便可求出平均每天耗资最少时试验的天数;(2)先求出实际耗资的连续函数,
天内总计的试验费用,然后再求出每天的平均试验费用,利用基本不等式便可求出平均每天耗资最少时试验的天数;(2)先求出实际耗资的连续函数,![]() ,讨论
,讨论![]() 和
和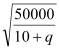 的大小关系即可解得
的大小关系即可解得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(1)依题意得,试验开始后,每天的试验费用构成等差数列,公差为![]() ,首项为
,首项为![]() ,
,
∴试验30天共花费试验费用为![]() ,
,
解得,![]() .............................2分
.............................2分
设试验![]() 天,平均每天耗资为
天,平均每天耗资为![]() 元,则
元,则
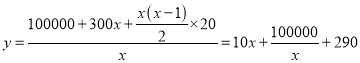 ..................4分
..................4分
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
综上得,![]() ,试验天数为100天..................................6分
,试验天数为100天..................................6分
(2)设平均每天实际耗资为![]() 元,则
元,则
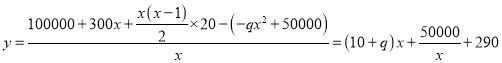 ...........8分
...........8分
当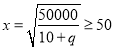 ,即
,即![]() 时,
时,
![]() ,因为
,因为![]() ,
,
所以,![]() ,.......................10分
,.......................10分
当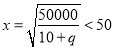 ,即
,即![]() 时,当
时,当![]() 时,
时,![]() 取最小值,
取最小值,
且![]() ,
,
综上得,![]() 的取值范围为
的取值范围为![]() ....................12分
....................12分

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目