题目内容
【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据题意,明确给定范围上的![]() 的表达式,然后求值域;(2)根据题意,明确给定范围上的
的表达式,然后求值域;(2)根据题意,明确给定范围上的![]() 的表达式,然后恒成立问题就转化为最值问题.
的表达式,然后恒成立问题就转化为最值问题.
试题解析:(1)设![]() ,.............1分
,.............1分
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减,.................2分
递减,.................2分
∴![]() ,∴
,∴![]() ,.......................3分
,.......................3分
即![]() ,∴
,∴![]() .............4分
.............4分
故函数![]() 在
在![]() 上的值域为
上的值域为![]() ...........................5分
...........................5分
(2)①当![]() 时,
时,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .................................................. 6分
.................................................. 6分
若![]() ,对
,对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减.
递减.
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ....9分
....9分
②当![]() 时,由(1)知
时,由(1)知![]() ,对
,对![]() 恒成立,
恒成立,
若![]() 对
对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,这显然不可能.
恒成立,这显然不可能.
即当![]() 时,不满足
时,不满足![]() 对
对![]() 恒成立,.........................11分
恒成立,.........................11分
故存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .......12分
.......12分

练习册系列答案
相关题目
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中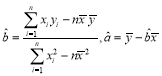 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
