题目内容
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)记![]() ,求函数
,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)若对任意的![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)2(3)
(2)2(3)![]()
【解析】
(1)先求导![]() ,根据函数
,根据函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,有
,有![]() 求解.
求解.
(2)由(1)得到![]() , 再利用导数法求其最小值.
, 再利用导数法求其最小值.
(3)先将对任意的![]() ,恒有
,恒有![]() ,转化为
,转化为![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,求导
,求导![]() ,根据(2)的结论,分当
,根据(2)的结论,分当![]() 和
和 ![]() ,两种情况讨论求解.
,两种情况讨论求解.
(1)因为![]() ,
,
所以![]() ,
,
因为函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,
,
解得![]() .
.
(2)![]() ,
,
![]()
因为![]() ,所以
,所以![]()
所以函数![]() 在
在![]() 上是增函数
上是增函数
所以函数![]() 在
在![]() 上的最小值
上的最小值![]() ;
;
(3)因为对任意的![]() ,恒有
,恒有![]() ,
,
所以![]() 对任意的
对任意的![]() 恒成立,
恒成立,
令![]() ,
,
![]() ,
,
由(2)知当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上是增函数.
上是增函数.
所以![]() 成立.
成立.
当![]() 时,则存在
时,则存在![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,矛盾.
,矛盾.
综上:![]() .
.

【题目】今年是新中国成立70周年.70年来,在中国共产党的坚强领导下,全国各族人民团结心,迎难而上,开拓进取,奋力前行,创造了一个又一个人类发展史上的伟大奇迹,中华民族迎来了从站起来、富起来到强起来的伟大飞跃.某公司统计了第![]() 年(2013年是第一年)的经济效益为
年(2013年是第一年)的经济效益为![]() (千万元),得到如下表格:
(千万元),得到如下表格:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
若由表中数据得到![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,则可预测2020年经济效益大约是( )
,则可预测2020年经济效益大约是( )
A.5.95千万元B.5.25千万元C.5.2千万元D.5千万元
【题目】冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有![]() 材料、
材料、![]() 材料供选择,研究人员对附着在
材料供选择,研究人员对附着在![]() 材料、
材料、![]() 材料上再结晶各做了50次试验,得到如下等高条形图.
材料上再结晶各做了50次试验,得到如下等高条形图.
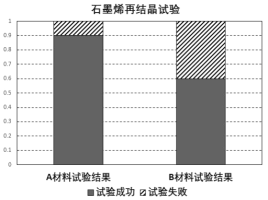
(1)根据上面的等高条形图,填写如下列联表,判断是否有99%的把握认为试验成功与材料有关?
|
| 合计 | |
成功 | |||
不成功 | |||
合计 |
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及![]() 胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为
胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为![]() ,第三个环节生产合格的概率为
,第三个环节生产合格的概率为![]() ,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
附:参考公式: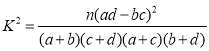 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |