题目内容
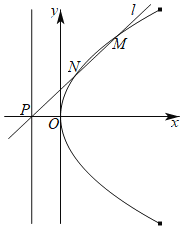
【题目】在直角坐标系xOy中,已知抛物线C:y2=2px(p>0)的焦点为F,过F垂直于x轴的直线与C相交于A、B两点,△AOB的面积为2.
(1)求抛物线C的方程;
(2)若过P(![]() ,0)的直线与C相交于M,N两点,且
,0)的直线与C相交于M,N两点,且![]() 2
2![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)y2=4x(2)![]() 或
或![]() .
.
【解析】
(1)先得出直线AB的方程,将直线AB的方程与抛物线C的方程联立,求出交点A、B的坐标,可求出|AB|,然后利用三角形的面积公式可求出p的值,即可求出抛物线的方程;
(2)设直线l的方程为x=my﹣1,设点M(x1,y1)、N(x2,y2),将直线l的方程与抛物线C的方程联立,并列出韦达定理,由![]() 得出y1=2y2,并将此关系式代入韦达定理,可求出m的值,即可得出直线l的方程.
得出y1=2y2,并将此关系式代入韦达定理,可求出m的值,即可得出直线l的方程.
(1)易知直线AB的方程为![]() ,将该直线方程代入抛物线C的方程得
,将该直线方程代入抛物线C的方程得![]() ,∴
,∴![]() 、
、![]() ,且|AB|=2p,
,且|AB|=2p,
∴△AOB的面积为![]() ,∵p>0,解得p=2.
,∵p>0,解得p=2.
因此,抛物线C的方程为y2=4x;
(2)设直线MN的方程为![]() ,设点M(x1,y1)、N(x2,y2),y2﹣4my+4=0
,设点M(x1,y1)、N(x2,y2),y2﹣4my+4=0
△=16m2﹣16>0,解得m<﹣1或m>1.
![]() ,
,![]() ,∵
,∵![]() ,∴y1=2y2,
,∴y1=2y2,
由韦达定理得y1+y2=3y2=4m,则![]() ,
,
![]() ,得
,得![]() ,
,
因此,直线l的方程为![]() ,即
,即![]() 或
或![]() .
.

 优学名师名题系列答案
优学名师名题系列答案【题目】语音交互是人工智能的方向之一,现在市场上流行多种可实现语音交互的智能音箱.主要代表有小米公司的“小爱同学”智能音箱和阿里巴巴的“天猫精灵”智能音箱,它们可以通过语音交互满足人们的部分需求.某经销商为了了解不同智能音箱与其购买者性别之间的关联程度,从某地区随机抽取了100名购买“小爱同学”和100名购买“天猫精灵”的人,具体数据如下:
“小爱同学”智能音箱 | “天猫精灵”智能音箱 | 合计 | |
男 | 45 | 60 | 105 |
女 | 55 | 40 | 95 |
合计 | 100 | 100 | 200 |
(1)若该地区共有13000人购买了“小爱同学”,有12000人购买了“天猫精灵”,试估计该地区购买“小爱同学”的女性比购买“天猫精灵”的女性多多少人?
(2)根据列联表,能否有95%的把握认为购买“小爱同学”、“天猫精灵”与性别有关?
附: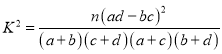
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |