题目内容
10．若直线 l1和l2 是异面直线，l1在平面 α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是（ ）| A． | l与l1，l2都不相交 | B． | l与l1，l2都相交 | ||
| C． | l至多与l1，l2中的一条相交 | D． | l至少与l1，l2中的一条相交 |
分析 可以画出图形来说明l与l1，l2的位置关系，从而可判断出A，B，C是错误的，而对于D，可假设不正确，这样l便和l1，l2都不相交，这样可推出和l1，l2异面矛盾，这样便说明D正确．
解答 解：A．l与l1，l2可以相交，如图：
∴该选项错误；
B．l可以和l1，l2中的一个平行，如上图，∴该选项错误；
C．l可以和l1，l2都相交，如下图：
，∴该选项错误；
D．“l至少与l1，l2中的一条相交”正确，假如l和l1，l2都不相交；
∵l和l1，l2都共面；
∴l和l1，l2都平行；
∴l1∥l2，l1和l2共面，这样便不符合已知的l1和l2异面；
∴该选项正确．
故选D．
点评 考查异面直线的概念，在直接说明一个命题正确困难的时候，可说明它的反面不正确．
练习册系列答案
相关题目
20．已知直线y=$\frac{1}{3}x+\frac{2}{3}$与幂函数f（x）=xm（m≠0）的图象将于A、B两点，且|AB|=$\sqrt{10}$，则m的值为（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
2．某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（ ）
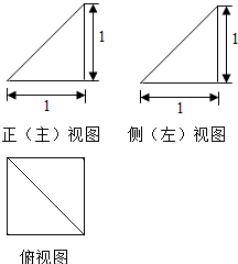
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
19．
一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ）
一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ）| A． | $\frac{1}{8}$ | B． | $\frac{1}{7}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{5}$ |
20．某工厂36名工人年龄数据如图：
（1）用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
（2）计算（1）中样本的均值$\overline{x}$和方差s2；
（3）36名工人中年龄在$\overline{x}$-s和$\overline{x}$+s之间有多少人？所占百分比是多少（精确到0.01%）？
| 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
| 1 2 3 4 5 6 7 8 9 | 40 44 40 41 33 40 45 42 43 | 10 11 12 13 14 15 16 17 18 | 36 31 38 39 43 45 39 38 36 | 19 20 21 22 23 24 25 26 27 | 27 43 41 37 34 42 37 44 42 | 28 29 30 31 32 33 34 35 36 | 34 39 43 38 42 53 37 49 39 |
（2）计算（1）中样本的均值$\overline{x}$和方差s2；
（3）36名工人中年龄在$\overline{x}$-s和$\overline{x}$+s之间有多少人？所占百分比是多少（精确到0.01%）？