题目内容

2．某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（　　）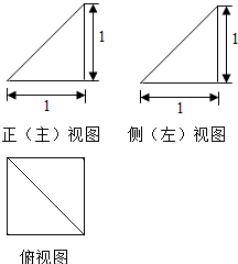
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2

分析 几何体是四棱锥，且四棱锥的一条侧棱与底面垂直，结合直观图求相关几何量的数据，可得答案

解答 解：由三视图知：几何体是四棱锥，且四棱锥的一条侧棱与底面垂直，
底面为正方形如图：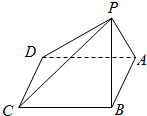
其中PB⊥平面ABCD，底面ABCD为正方形
∴PB=1，AB=1，AD=1，
∴BD=$\sqrt{2}$，PD=$\sqrt{2+1}$=$\sqrt{3}$．
PC==$PA=\sqrt{2}$
该几何体最长棱的棱长为：$\sqrt{3}$
故选：C．

点评 本题考查了由三视图求几何体的最长棱长问题，根据三视图判断几何体的结构特征是解答本题的关键

练习册系列答案
相关题目
12．已知△ABC中，a=3${\;}^{\frac{1}{2}}$，$\frac{b+c}{a}$=$\frac{2-cosB-cosC}{cosA}$，求三角形周长．
13．观察下列各式：
C${\;}_{1}^{0}$=40；
C${\;}_{3}^{0}$+C${\;}_{3}^{1}$=41；
C${\;}_{5}^{0}$+C${\;}_{5}^{1}$+C${\;}_{5}^{2}$=42；
C${\;}_{7}^{0}$+C${\;}_{7}^{1}$+C${\;}_{7}^{2}$+C${\;}_{7}^{3}$=43；
…
照此规律，当n∈N*时，
C${\;}_{2n-1}^{0}$+C${\;}_{2n-1}^{1}$+C${\;}_{2n-1}^{2}$+…+C${\;}_{2n-1}^{n-1}$=4n-1．
10．若直线 l1和l2 是异面直线，l1在平面 α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是（　　）
A．l与l1，l2都不相交B．l与l1，l2都相交
C．l至多与l1，l2中的一条相交D．l至少与l1，l2中的一条相交
17．某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．

（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，[220，240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？
7．设函数f（x）=$\frac{{x}^{2}}{2}$-klnx，k＞0．
（1）求f（x）的单调区间和极值；
（2）证明：若f（x）存在零点，则f（x）在区间（1，$\sqrt{e}$]上仅有一个零点．
14．设△ABC的内角A，B，C的对边分别为a，b，c，a=btanA．
（Ⅰ）证明：sinB=cosA；
（Ⅱ）若sinC-sinAcosB=$\frac{3}{4}$，且B为钝角，求A，B，C．
11．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-4≤0}\\{y≥1}\end{array}\right.$，则z=-2x+y的最大值是（　　）
A．-1B．-2C．-5D．1
12．设复数z=（x-1）+yi（x，y∈R），若|z|≤1，则y≥x的概率为（　　）
A．$\frac{3}{4}$+$\frac{1}{2π}$B．$\frac{1}{2}$+$\frac{1}{π}$C．$\frac{1}{2}$-$\frac{1}{π}$D．$\frac{1}{4}$-$\frac{1}{2π}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网