题目内容
2.数列{an}的通项公式an=$\root{n}{n}$,用二项式定理证明an<$\sqrt{\frac{2}{n}}$+1.分析 要证an<$\sqrt{\frac{2}{n}}$+1,即证$\root{n}{n}$<$\sqrt{\frac{2}{n}}$+1,也就是证n<($\sqrt{\frac{2}{n}}$+1)n,再利用二项式定理即可证明.
解答 证明:要证an<$\sqrt{\frac{2}{n}}$+1,即证$\root{n}{n}$<$\sqrt{\frac{2}{n}}$+1,
也就是证n<($\sqrt{\frac{2}{n}}$+1)n,
当n=1时,1<$\sqrt{2}$+1,显然成立;
当n=2时,2<(1+1)2=4,显然成立;
当n≥3时,($\sqrt{\frac{2}{n}}$+1)n=(1+$\sqrt{\frac{2}{n}}$)n=${C}_{n}^{0}$+${C}_{n}^{1}$$\sqrt{\frac{2}{n}}$+${C}_{n}^{2}$($\sqrt{\frac{2}{n}}$)2+…
>1+$\sqrt{2n}$+(n-1)>1+n-1=n,
综合以上情形,故有an<$\sqrt{\frac{2}{n}}$+1.
点评 本题考查二项式定理证明不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知圆C:x2+y2-4x-4y=0与x轴相交于A,B两点,则弦AB所对的圆心角的大小( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
10.我们把焦距和短轴相等的椭圆称为“等轴椭圆”.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,一“等轴椭圆”与该双曲线有相同的焦点,且双曲线的渐近线与椭圆相交于第一象限内的一点M,若直线F1M的斜率为$\frac{\sqrt{2}}{4}$,则该双曲线的离心率为( )
| A. | $\frac{3\sqrt{22}}{14}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{22}}{14}$或$\frac{\sqrt{6}}{2}$ |
8.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
 中,
中, ,
, ,求此数列的通项公式.
,求此数列的通项公式.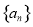 的公差为
的公差为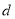 ,前
,前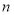 项和为
项和为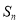 ,若
,若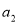 ,
,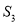 ,
,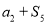 成等比数列,则
成等比数列,则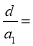 ( )
( )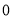 B.
B.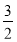
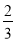 D.
D.