题目内容
7.将《格林童话》、《安徒生童话》、《西游记》、《三国演义》、《老夫子》、《天使街23号》这6本书赠给某希望工程学校的4名学生阅读,每人至少1本,至多2本,则恰好有1人同时获得《格林童话》、《安徒生童话》两本书的概率是$\frac{2}{15}$.分析 先设“恰有一人获得《格林童话》、《安徒生童话》两本书”为事件A,然后求出恰有一人获得《格林童话》、《安徒生童话》两本书的事件个数,再求出6本书分给4个阅读的事件个数,相除即可.
解答 解:记“恰有一人获得《格林童话》、《安徒生童话》两本书”为事件A,
恰有一人获得《格林童话》、《安徒生童话》两本书的事件共有:${C}_{4}^{1}•{C}_{4}^{2}•{A}_{3}^{3}$=144种,
6本书分给4个阅读,每人至少1本,至多2本,即每个人分到2,2,1,1本书,
6本书分给4个阅读的事件共有:${C}_{6}^{2}•{C}_{4}^{2}•{A}_{4}^{4}$÷2=1080种
则P(A)=$\frac{144}{1080}$=$\frac{2}{15}$
故答案为:$\frac{2}{15}$.
点评 本题考查了排列组合的知识,考查了学生分析问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732.
要设计一个隧道,在隧道内设双行线公路,其截面由一个长方形和抛物线构成(如图所示),若车道总宽度AB为6m,通过车辆(设为平顶)限高3.5米,且车辆顶部与隧道顶部在竖直方向上的高度只差至少为0.5m,则隧道的拱宽CD至少应设计为(精确到0.1m.)( )参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732. .
. 是不是该数列中的项,为什么?
是不是该数列中的项,为什么? 内有、无数列中的项?若有,有几项?若没有,说明理由.
内有、无数列中的项?若有,有几项?若没有,说明理由. 满足
满足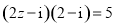 ,则
,则 ( )
( ) B.
B.
 D.
D.