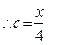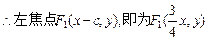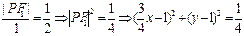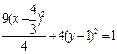题目内容
求经过点P(1,1),以y轴为准线,离心率为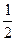 的椭圆的中心的轨迹方程
的椭圆的中心的轨迹方程
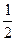 的椭圆的中心的轨迹方程
的椭圆的中心的轨迹方程椭圆的中心的轨迹方程是: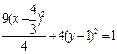
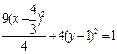
因为椭圆经过点P(1,1),又以y轴为准线,所以椭圆在y轴的右边.
设椭圆中心Q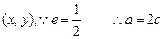 .
.
而中心Q到准线的距离为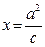 .
. 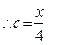
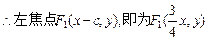
由椭圆的第二定义得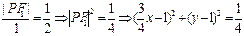
即椭圆的中心的轨迹方程是: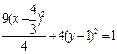
设椭圆中心Q
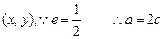 .
. 而中心Q到准线的距离为
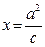 .
. 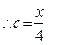
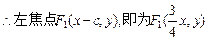
由椭圆的第二定义得
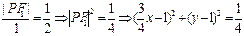
即椭圆的中心的轨迹方程是:
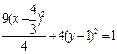

练习册系列答案
相关题目
题目内容
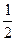 的椭圆的中心的轨迹方程
的椭圆的中心的轨迹方程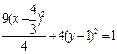
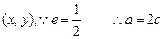 .
. 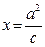 .
.