题目内容
(本题满分14分)已知直角坐标平面内点
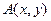 到点
到点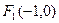 与点
与点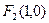 的距离之和为
的距离之和为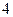
(Ⅰ)试求点
 的轨迹
的轨迹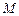 的方程;
的方程;(Ⅱ)若斜率为
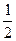 的直线
的直线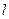 与轨迹
与轨迹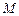 交于
交于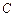 、
、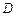 两点,点
两点,点 为轨迹
为轨迹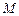 上一点,记直线
上一点,记直线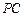 的斜率为
的斜率为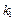 ,直线
,直线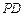 的斜率为
的斜率为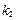 ,试问:
,试问: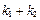 是否为定值?请证明你的结论.
是否为定值?请证明你的结论. ,是
,是解:(Ⅰ) 由题知 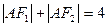 ,
, 则
则 ………2分
………2分
由椭圆的定义知点 轨迹
轨迹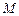 是椭圆…………3分
是椭圆…………3分
其中 .因为
.因为  ,…5分
,…5分
所以,轨迹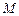 的方程为
的方程为 …6分
…6分
(Ⅱ)设直线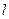 的方程为:
的方程为: ,
,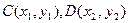
联立直线 的方程与
的方程与 椭圆方程得:
椭圆方程得:

(1)代入(2)得:
化简得: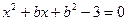 ………(3) ……………8分
………(3) ……………8分
当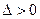 时,即,
时,即,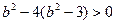 也即,
也即,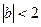 时,直线
时,直线 与椭圆有两交点,
与椭圆有两交点,
由韦达定理得: , ………………10分
, ………………10分
所以, ,
, 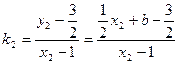
则


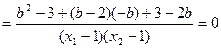 ……………13分
……………13分
所以, 为定值。 ……………14分
为定值。 ……………14分
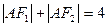 ,
, 则
则 ………2分
………2分由椭圆的定义知点
 轨迹
轨迹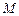 是椭圆…………3分
是椭圆…………3分其中
 .因为
.因为  ,…5分
,…5分所以,轨迹
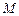 的方程为
的方程为 …6分
…6分(Ⅱ)设直线
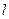 的方程为:
的方程为: ,
,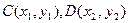
联立直线
 的方程与
的方程与 椭圆方程得:
椭圆方程得:
(1)代入(2)得:

化简得:
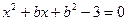 ………(3) ……………8分
………(3) ……………8分当
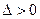 时,即,
时,即,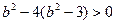 也即,
也即,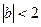 时,直线
时,直线 与椭圆有两交点,
与椭圆有两交点, 由韦达定理得:
 , ………………10分
, ………………10分所以,
 ,
, 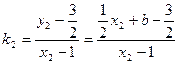
则



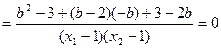 ……………13分
……………13分所以,
 为定值。 ……………14分
为定值。 ……………14分
练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
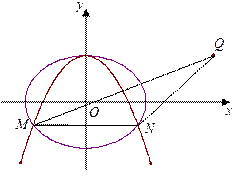
 :
: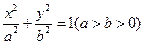 ,抛物线
,抛物线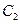 :
: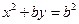 .
.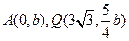 ,又
,又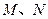 为
为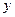 轴上的两个交点,若
轴上的两个交点,若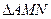 的垂心为
的垂心为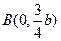 ,且
,且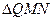 的重心在
的重心在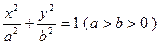 ,它的一个顶点为
,它的一个顶点为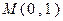 ,离心率
,离心率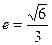 .
. 与椭圆交于A,B两点,坐标原点O到直线l的距离为
与椭圆交于A,B两点,坐标原点O到直线l的距离为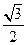 ,求△AOB面积的最大值.
,求△AOB面积的最大值.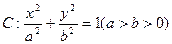 的左、右焦点分别为F1与F2,直线
的左、右焦点分别为F1与F2,直线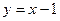 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若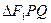 的周长为
的周长为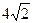 。
。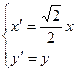 变成曲线
变成曲线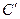 ,直线
,直线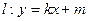 与曲线
与曲线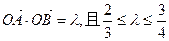 ,求
,求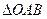 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 的方程是
的方程是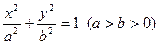 ,椭圆的左顶点为
,椭圆的左顶点为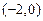 ,离心率
,离心率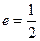 ,倾斜角为
,倾斜角为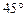 的直线
的直线 与椭圆交于
与椭圆交于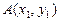 、
、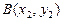 两点.
两点. (
(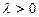 ),若点
),若点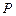 在椭圆
在椭圆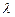 的取值范围.
的取值范围.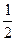 的椭圆的中心的轨迹方程
的椭圆的中心的轨迹方程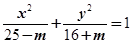 表示焦点在y轴上的椭圆,则m的取值范围为 .
表示焦点在y轴上的椭圆,则m的取值范围为 .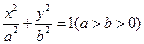 的右焦点且垂直于
的右焦点且垂直于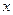 轴的直线与椭圆交于
轴的直线与椭圆交于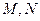 两点,以
两点,以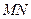 为直径的圆恰好过左焦点,则椭圆的离心率等于 。
为直径的圆恰好过左焦点,则椭圆的离心率等于 。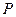 是以
是以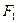 ,
,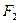 为焦点的椭圆
为焦点的椭圆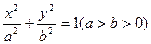 上的一点,若
上的一点,若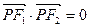 ,
,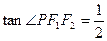 ,则此椭圆的离心率为____________.
,则此椭圆的离心率为____________.