题目内容
已知椭圆C：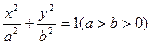
的左、右焦点为F1、F2，离心率为e. 直线
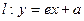与x轴、y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设
（Ⅰ）证明：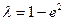
；
（Ⅱ）若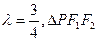
的周长为6；写出椭圆C的方程.
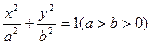的左、右焦点为F1、F2，离心率为e. 直线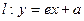与x轴、y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设（Ⅰ）证明：
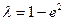；（Ⅱ）若
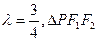的周长为6；写出椭圆C的方程. （Ⅰ）见解析
（Ⅱ）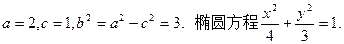
（Ⅱ）
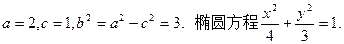
（Ⅰ）证法一：因为A、B分别是直线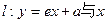
轴、y轴的交点，
所以A、B的坐标分别是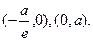
…………2分
由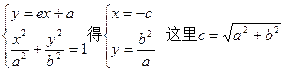
…………4分
所以点M的坐标是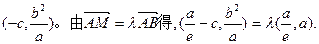
即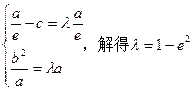
………………6分
证法二：因为A、B分别是直线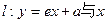轴、y轴的交点，所以A、B的坐标分别是 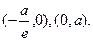………………2分
设M的坐标是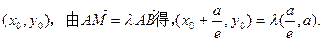
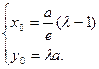………………4分
因为点M在椭圆上，所以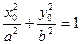
即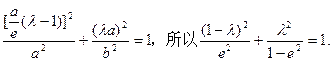
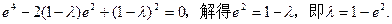…………6分
（Ⅱ）当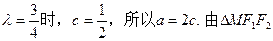
的周长为6，得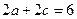
所以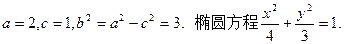
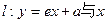轴、y轴的交点，所以A、B的坐标分别是
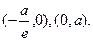…………2分由
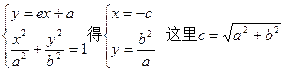…………4分所以点M的坐标是
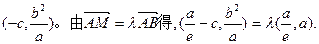
即
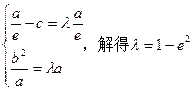………………6分证法二：因为A、B分别是直线
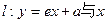轴、y轴的交点，所以A、B的坐标分别是 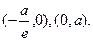………………2分设M的坐标是
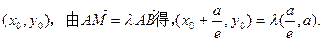
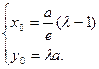………………4分因为点M在椭圆上，所以
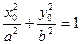
即
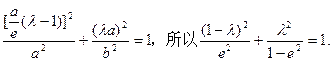
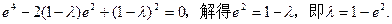…………6分（Ⅱ）当
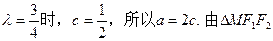的周长为6，得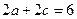所以
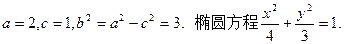
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
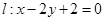与坐标轴的交点分别是一个椭圆的焦点和顶点，则此椭圆的离心率为 （ ）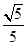
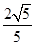
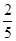
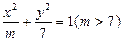上一点P到右焦点的距离是长轴两端点到右焦点距离的等差中项，则P点的坐标为 . 
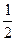的椭圆的中心的轨迹方程
、
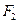分别是椭圆
的左、右焦点. 
的最大值和最小值；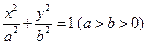
的左焦点
作x轴的垂线交椭圆于点P，点A和点B分别为椭圆的右顶点和上顶点，OP∥AB．
（2）过右焦点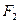
作一条弦QR，使QR⊥AB．若△
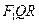的面积为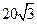
，求椭圆的方程．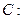
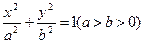的离心率为
=
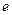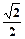,点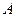
是椭圆上的一点,且点
两焦点的距离之和为4.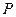
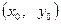关于直线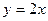
的对称点为
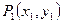,求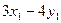
的取值范围.
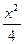+y2=1的左、右焦点,点P在椭圆上运动,则|PF1|·|PF2|的最大值是_________________.
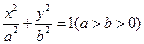的右焦点且垂直于
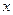轴的直线与椭圆交于
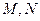两点，以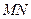
为直径的圆恰好过左焦点，则椭圆的离心率等于 。