题目内容
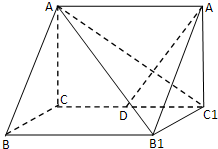
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1,AA1=
,D是棱CC1的中点.
(Ⅰ)证明:A1D⊥平面AB1C1;
(Ⅱ)求平面A1B1A与平面AB1C1所成的锐二面角的余弦值.
| 6 |
(Ⅰ)证明:A1D⊥平面AB1C1;
(Ⅱ)求平面A1B1A与平面AB1C1所成的锐二面角的余弦值.

(Ⅰ)∵∠ACB=90°,∴BC⊥AC.
∵三棱柱ABC-A1B1C1中,CC1⊥平面ABC.∴BC⊥CC1,
∵AC∩CC1=C,∴BC⊥平面ACC1A1.
∵A1D?平面ACC1A1,∴BC⊥A1D,而BC∥B1C1,则B1C1⊥A1D.
在Rt△ACC1与Rt△DC1A1中,
=
=
,∴△ACC1~△DC1A1,
∴∠AC1C=∠DA1C1.∴∠AC1C+∠C1DA1=90°.即A1D⊥AC1.
∵B1C1∩AC1=C1,∴A1D⊥平面AB1C1.
(Ⅱ)如图,设A1D∩AC1=H,过A1作AB1的垂线,垂足为G,连GH,
∵A1D⊥平面AB1C1,∴AB1⊥A1D,∴AB1⊥平面A1GH∴∠A1GH为二面角A1-AB1-C1的平面角.
在Rt△AA1B1中,AA1=
,A1B1=2,∴AB1=
,∴A1G=
=
;
在Rt△AA1C1中,AA1=
,A1C1=
,∴AC1=3,∴A1H=
=
.
∴在Rt△A1GH中,sin∠A1GH=
=
=
,cos∠A1GH=
.
故锐二面角A1-AB1-C1的余弦值为
.
即平面A1B1A与平面AB1C1所成的锐二面角的余弦值为
.

∵三棱柱ABC-A1B1C1中,CC1⊥平面ABC.∴BC⊥CC1,
∵AC∩CC1=C,∴BC⊥平面ACC1A1.
∵A1D?平面ACC1A1,∴BC⊥A1D,而BC∥B1C1,则B1C1⊥A1D.
在Rt△ACC1与Rt△DC1A1中,
| AC |
| CC1 |
| DC1 |
| AC1 |
| ||
| 2 |
∴∠AC1C=∠DA1C1.∴∠AC1C+∠C1DA1=90°.即A1D⊥AC1.
∵B1C1∩AC1=C1,∴A1D⊥平面AB1C1.
(Ⅱ)如图,设A1D∩AC1=H,过A1作AB1的垂线,垂足为G,连GH,
∵A1D⊥平面AB1C1,∴AB1⊥A1D,∴AB1⊥平面A1GH∴∠A1GH为二面角A1-AB1-C1的平面角.
在Rt△AA1B1中,AA1=
| 6 |
| 10 |
| AA1•A1B1 |
| AB1 |
2
| ||
| 5 |
在Rt△AA1C1中,AA1=
| 6 |
| 3 |
| AA1•A1C1 |
| AC1 |
| 2 |
∴在Rt△A1GH中,sin∠A1GH=
| A1H |
| A1G |
5
| ||
2
|
| ||
| 6 |
| ||
| 6 |
故锐二面角A1-AB1-C1的余弦值为
| ||
| 6 |
即平面A1B1A与平面AB1C1所成的锐二面角的余弦值为
| ||
| 6 |


练习册系列答案
相关题目





 与
与 满足
满足 ,
, ,若存在实数
,若存在实数 ,使得
,使得 垂直,则
垂直,则
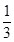 e2-e1共线,则实数λ=( )
e2-e1共线,则实数λ=( ) ,P为BE上一点,且满足
,P为BE上一点,且满足 ,则
,则 取最小值时,向量
取最小值时,向量 的模为 .
的模为 .