题目内容
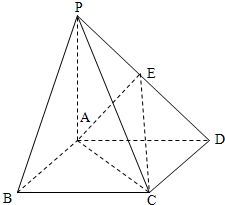
在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD,且PA=2AB.(1)求证:BD⊥PC;
(2)求三棱锥A-PCD的体积;
(3)求二面角B-PC-D的余弦值.

(2)求三棱锥A-PCD的体积;
(3)求二面角B-PC-D的余弦值.

(1)证明:如图所示,连接BD交AC于点O.
∵四边形ABCD是正方形,∴BD⊥AC.
∵PA⊥底面ABCD,∴PA⊥BD.
又AC∩BD=O.
∴BD⊥平面PAC,∴BD⊥PC.
(2)∵PA⊥底面ABCD,∴PA=2a是四棱锥P-ACD的高.
而S△ACD=
AD•CD=
a2.
∴V四棱锥P-ACD=
S△ACD•PA=
•
a2•2a=
a3.
(3)建立如图所示的空间直角坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,2a).
则
=(0,a,0),
=(a,a,-2a),
=(a,0,0).
设平面PAC的法向量为
=(x,y,z),则
,令x=2,则y=0,z=1,∴
=(2,0,1).
同理可得平面PCD的法向量
=(0,2,1).
∴cos<
,
>=
=
=
.
由图形可知:二面角B-PC-D的平面角是钝角,故其余弦值为-
.

∵四边形ABCD是正方形,∴BD⊥AC.
∵PA⊥底面ABCD,∴PA⊥BD.
又AC∩BD=O.
∴BD⊥平面PAC,∴BD⊥PC.
(2)∵PA⊥底面ABCD,∴PA=2a是四棱锥P-ACD的高.
而S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴V四棱锥P-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(3)建立如图所示的空间直角坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,2a).
则
| BC |
| PC |
| DC |
设平面PAC的法向量为
| m |
|
| m |
同理可得平面PCD的法向量
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 5 |
由图形可知:二面角B-PC-D的平面角是钝角,故其余弦值为-
| 1 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是平行四边形
是平行四边形 平面外一点,
平面外一点, 分别是
分别是 上的点,且
上的点,且 =
= , 求证:
, 求证: 平面
平面