题目内容
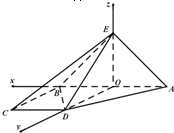
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
(Ⅰ)求证:AB⊥DE;
(Ⅱ)求直线EC与平面ABE所成角的正弦值;
(Ⅲ)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出
;若不存在,说明理由.

(Ⅰ)求证:AB⊥DE;
(Ⅱ)求直线EC与平面ABE所成角的正弦值;
(Ⅲ)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出
| EF |
| EA |

(Ⅰ)证明:取AB中点O,连接EO,DO.
因为EB=EA,所以EO⊥AB.…(1分)
因为四边形ABCD为直角梯形,AB=2CD=2BC,AB⊥BC,
所以四边形OBCD为正方形,所以AB⊥OD.…(2分)
因为EO∩OD=O
所以AB⊥平面EOD.…(3分)
因为ED?平面EOD
所以AB⊥ED.…(4分)
(Ⅱ)因为平面ABE⊥平面ABCD,且EO⊥AB,平面ABE∩平面ABCD=AB
所以EO⊥平面ABCD,
因为OD?平面ABCD,所以EO⊥OD.
由OB,OD,OE两两垂直,建立如图所示的空间直角坐标系O-xyz.…(5分)
因为△EAB为等腰直角三角形,所以OA=OB=OD=OE,设OB=1,所以O(0,0,0),A(-1,0,0),B(1,0,0),C(1,1,0),D(0,1,0),E(0,0,1).
所以
=(1,1,-1),平面ABE的一个法向量为
=(0,1,0).…(7分)
设直线EC与平面ABE所成的角为θ,
所以sinθ=|cos?
,
>|=
=
,
即直线EC与平面ABE所成角的正弦值为
.…(9分)
(Ⅲ)存在点F,且
=
时,有EC∥平面FBD.…(10分)
证明如下:由
=
=(-
,0,-
),F(-
,0,
),所以
=(
,0,-
).
设平面FBD的法向量为
=(a,b,c),则有
所以
取a=1,得
=(1,1,2).…(12分)
因为
•
=(1,1,-1)•(1,1,2)=0,且EC?平面FBD,所以EC∥平面FBD.
即点F满足
=
时,有EC∥平面FBD.…(14分)
因为EB=EA,所以EO⊥AB.…(1分)
因为四边形ABCD为直角梯形,AB=2CD=2BC,AB⊥BC,
所以四边形OBCD为正方形,所以AB⊥OD.…(2分)
因为EO∩OD=O
所以AB⊥平面EOD.…(3分)
因为ED?平面EOD
所以AB⊥ED.…(4分)
(Ⅱ)因为平面ABE⊥平面ABCD,且EO⊥AB,平面ABE∩平面ABCD=AB
所以EO⊥平面ABCD,
因为OD?平面ABCD,所以EO⊥OD.
由OB,OD,OE两两垂直,建立如图所示的空间直角坐标系O-xyz.…(5分)
因为△EAB为等腰直角三角形,所以OA=OB=OD=OE,设OB=1,所以O(0,0,0),A(-1,0,0),B(1,0,0),C(1,1,0),D(0,1,0),E(0,0,1).
所以
| EC |
| OD |
设直线EC与平面ABE所成的角为θ,
所以sinθ=|cos?
| EC |
| OD |
|
| ||||
|
|
| ||
| 3 |
即直线EC与平面ABE所成角的正弦值为
| ||
| 3 |
(Ⅲ)存在点F,且
| EF |
| EA |
| 1 |
| 3 |
证明如下:由
| EF |
| 1 |
| 3 |
| EA |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| FB |
| 4 |
| 3 |
| 2 |
| 3 |
设平面FBD的法向量为
| v |
|
所以
|
| v |
因为
| EC |
| v |
即点F满足
| EF |
| EA |
| 1 |
| 3 |


练习册系列答案
相关题目



 ,
, ,则
,则 的最小值是( )
的最小值是( )

 =a,
=a, =b,
=b, =c.点M在OA上,且OM=2MA,N为BC的中点,则
=c.点M在OA上,且OM=2MA,N为BC的中点,则 等于( )
等于( )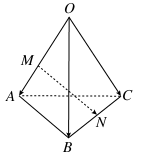
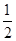 a-
a-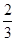 b+
b+