题目内容
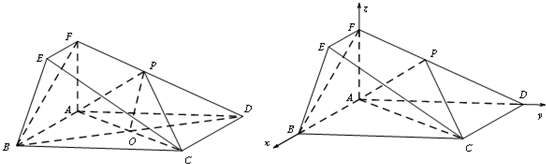
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
(Ⅰ)若P是DF的中点,
(ⅰ)求证:BF∥平面ACP;
(ⅱ)求异面直线BE与CP所成角的余弦值;
(Ⅱ)若二面角D-AP-C的余弦值为
,求PF的长度.

(Ⅰ)若P是DF的中点,
(ⅰ)求证:BF∥平面ACP;
(ⅱ)求异面直线BE与CP所成角的余弦值;
(Ⅱ)若二面角D-AP-C的余弦值为
| ||
| 3 |

(Ⅰ)(ⅰ)证明:连接BD,交AC于点O,连接OP.
因为P是DF中点,O为矩形ABCD对角线的交点,所以OP为三角形BDF中位线,所以BF∥OP,
因为BF?平面ACP,OP?平面ACP,所以BF∥平面ACP.…(4分)
(ⅱ)因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(
,0,1),P(0,1,
),C(1,2,0).
所以
=(-
,0,1),
=(-1,-1,
),
所以cos<
,
>=
=
,
即异面直线BE与CP所成角的余弦值为
.…(9分)
(Ⅱ)因为AB⊥平面ADF,所以平面APF的法向量为
=(1,0,0).
设P点坐标为(0,2-2t,t),在平面APC中,
=(0,2-2t,t),
=(1,2,0),
所以平面APC的法向量为
=(-2,1,
),
所以cos<
,
>=
=
=
,
解得t=
,或t=2(舍).
此时|PF|=
.…(14分)
因为P是DF中点,O为矩形ABCD对角线的交点,所以OP为三角形BDF中位线,所以BF∥OP,
因为BF?平面ACP,OP?平面ACP,所以BF∥平面ACP.…(4分)
(ⅱ)因为∠BAF=90°,所以AF⊥AB,
因为平面ABEF⊥平面ABCD,且平面ABEF∩平面ABCD=AB,所以AF⊥平面ABCD,
因为四边形ABCD为矩形,所以以A为坐标原点,AB,AD,AF分别为x,y,z轴,建立如图所示空间直角坐标系O-xyz.
所以B(1,0,0),E(
| 1 |
| 2 |
| 1 |
| 2 |
所以
| BE |
| 1 |
| 2 |
| CP |
| 1 |
| 2 |
所以cos<
| BE |
| CP |
| ||||
|
4
| ||
| 15 |
即异面直线BE与CP所成角的余弦值为
4
| ||
| 15 |

(Ⅱ)因为AB⊥平面ADF,所以平面APF的法向量为
| n1 |
设P点坐标为(0,2-2t,t),在平面APC中,
| AP |
| AC |
所以平面APC的法向量为
| n2 |
| 2t-2 |
| t |
所以cos<
| n1 |
| n2 |
|
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
解得t=
| 2 |
| 3 |
此时|PF|=
| ||
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 |=|
|=| |=|
|=| |,
|, ,且
,且 ,则点O,N,P依次是△ABC的( )
,则点O,N,P依次是△ABC的( )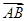 =a,
=a,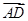 =b,
=b,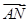 =3
=3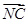 ,M为BC的中点,则
,M为BC的中点,则 =________(用a,b表示).
=________(用a,b表示). ,
, ,且
,且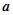 ∥
∥ ,则
,则 .
.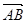 +
+ +
+ = .
= .