题目内容
如图,在△ABC中,∠C=90°,AC=BC=a,点P在边AB上,设
=λ
(λ>0),过点P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE将△APE翻折成△A′PE使平面A′PE⊥平面ABC;沿PE将△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
(1)求证:B′C∥平面A′PE;
(2)是否存在正实数λ,使得二面角C-A′B′-P的大小为90°?若存在,求出λ的值;若不存在,请说明理由.

| AP |
| PB |
(1)求证:B′C∥平面A′PE;
(2)是否存在正实数λ,使得二面角C-A′B′-P的大小为90°?若存在,求出λ的值;若不存在,请说明理由.

(1)证明:以C为原点,CB所在直线为x轴,CA所在直线为y轴,过C且垂直于平面ABC的直线为z轴,建立空间直角坐标系,如图,
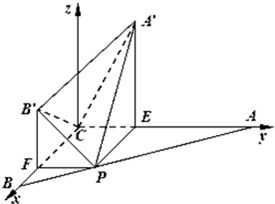
则C(0,0,0),A(0,a,0),B(a,0,0)设P(x,y,0),
由
=λ
⇒(x,y-a,0)=λ(a-x,-y,0)⇒x=
,y=
,
∴P(
,
,0),
从而E(0,
,0),F(
,0,0),
于是A′(0,
,
),B′(
,0,
),
平面A'PE的一个法向量为
=(0,
,0),
又
=(
,0,
),
•
=0,从而B'C∥平面A'PE.
(2)由(1)知有:
=(0,
,
),
=(
,-
,
),
=(0,
,-
).
设平面CA'B'的一个法向量为
=(x,y,-1),则
,
∴可得平面CA'B'的一个法向量
=(
,λ,-1),
同理可得平面PA'B'的一个法向量
=(1,1,1),
由
•
=0,即
+λ-1=0,
又λ>0,λ2-λ+1=0,由于△=-3<0,
∴不存在正实数λ,使得二面角C-A'B'-P的大小为90°.

则C(0,0,0),A(0,a,0),B(a,0,0)设P(x,y,0),
由
| AP |
| PB |
| λa |
| λ+1 |
| a |
| λ+1 |
∴P(
| λa |
| λ+1 |
| a |
| λ+1 |
从而E(0,
| a |
| λ+1 |
| λa |
| λ+1 |
于是A′(0,
| a |
| λ+1 |
| λa |
| λ+1 |
| λa |
| λ+1 |
| a |
| λ+1 |
平面A'PE的一个法向量为
| CE |
| a |
| λ+1 |
又
| CB′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| CB′ |
| CE |
(2)由(1)知有:
| CA′ |
| a |
| λ+1 |
| λa |
| λ+1 |
| A′B′ |
| λa |
| λ+1 |
| a |
| λ+1 |
| (1-λ)a |
| λ+1 |
| B′P |
| a |
| λ+1 |
| a |
| λ+1 |
设平面CA'B'的一个法向量为
| m |
|
∴可得平面CA'B'的一个法向量
| m |
| 1 |
| λ |
同理可得平面PA'B'的一个法向量
| n |
由
| m |
| n |
| 1 |
| λ |
又λ>0,λ2-λ+1=0,由于△=-3<0,
∴不存在正实数λ,使得二面角C-A'B'-P的大小为90°.

练习册系列答案
相关题目




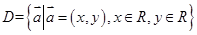 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 当且仅当“
当且仅当“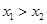 ”或“
”或“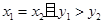 ”.按上述定义的关系“
”.按上述定义的关系“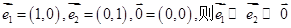 ;
;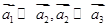 ,则
,则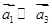 ;
;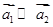 ,则对于任意
,则对于任意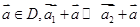 ;
;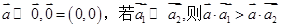 .
.