题目内容
9．设F为抛物线C：y2=4x的焦点，过F且倾斜角为45°的直线交C于A，B两点，则|AB|=（ ）| A． | 7 | B． | 8 | C． | 9 | D． | 10 |
分析 先根据抛物线方程求得焦点坐标和准线方程，根据直线的斜率求得直线的方程与抛物线方程联立消去y，根据韦达定理求得xA+xB的值，进而根据抛物线的定义可知直线AB的长为xA+$\frac{p}{2}$+xB+$\frac{p}{2}$答案可得．
解答 解：依题意可知抛物线C：y2=4x焦点为（1，0），直线AB的方程为y=x-1，代入抛物线方程得x2-6x+1=0，
∴xA+xB=3
根据抛物线的定义可知直线AB的长为：xA+$\frac{p}{2}$+xB+$\frac{p}{2}$=6+2=8．
故选：B．
点评 本题主要考查了抛物线的简单性质，直线与抛物线的位置关系．在涉及焦点弦的问题时常需要把直线与抛物线方程联立利用韦达定理设而不求，考查抛物线的定义的灵活应用．
练习册系列答案
相关题目
4．已知a=0.80.2，b=0.80.5，c=5.20.1，则这三个数的大小关系为（ ）
| A． | b＜a＜c | B． | a＜b＜c | C． | c＜a＜b | D． | c＜b＜a |
1．
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）
如图，从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x 轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
18．函数y=f（x）的图象如图所示，则以下描述正确的是（ ）
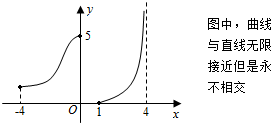
| A． | 函数f（x）的定义域为[-4，4） | |
| B． | 函数f（x）的值域为[0，5] | |
| C． | 此函数在定义域内既不是增函数也不是减函数 | |
| D． | 对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |