题目内容
【题目】直线y=x+b与曲线x= 
恰有一个公共点，则b的取值范围是 ．
【答案】﹣3＜b≤3或 
【解析】解：依题意可知曲线C的方程可整理成y2+x2=9（x≥0） 要使直线l与曲线c仅有一个公共点，有两种情况：如下图：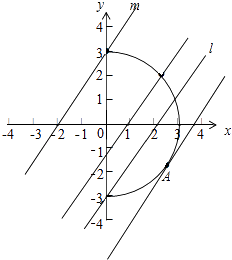
（i）直线与半圆相切，原点到直线的距离为3，切于A点，d= 
=3，因为b＜0，可得b=﹣3 
，满足题意；
（ii）直线过半圆的下顶点（0，﹣3）和过半圆的上顶点（0，3）之间的直线都满足，
y=x+b过点（0，﹣3），可得b=﹣3，有两个交点，
y=x+b过点（0，3），可得b=3，有一个交点，
∴﹣3＜b≤3，此时直线y=x+b与曲线x= 
恰有一个公共点；
综上：﹣3＜b≤3或 ．
所以答案是：﹣3＜b≤3或 ．
【考点精析】掌握函数的零点是解答本题的根本，需要知道函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点．
练习册系列答案
相关题目
