题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点(
两点(![]() ,
, ![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() .直线
.直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.设直线
两点.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(Ⅰ)由离心率![]() 可得
可得![]() ,由对称性直线
,由对称性直线![]() 被椭圆截得弦长为
被椭圆截得弦长为![]() 可求得
可求得![]() 点坐标为
点坐标为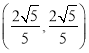 ,代入椭圆方程可求得
,代入椭圆方程可求得![]() 得椭圆标准方程;
得椭圆标准方程;
(Ⅱ)直线与椭圆相交,设![]() ,
, ![]() ,有
,有![]() ,由直线垂直得直线
,由直线垂直得直线![]() 的斜率为
的斜率为![]() .为了简便设直线
.为了简便设直线![]() 的方程为
的方程为![]() ,代入椭圆方程消元得
,代入椭圆方程消元得![]() 的一元二次方程.可得
的一元二次方程.可得![]() ,于是有
,于是有![]() ,而
,而![]() ,于是写出直线
,于是写出直线![]() 方程,求出
方程,求出![]() 点坐标,可得
点坐标,可得![]() ,比较可得
,比较可得![]() .
.
试题解析:
(Ⅰ)∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .①
.①
设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,不妨设点
两点,不妨设点![]() 为第一象限内的交点.∴
为第一象限内的交点.∴![]() ,
,
∴![]() 代入椭圆方程可得
代入椭圆方程可得![]() .②
.②
由①②知![]() ,
,![]() ,所以椭圆的方程为:
,所以椭圆的方程为:![]() .
.
(Ⅱ)设![]()
![]() ,则
,则![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,又
,又![]() ,
,
故直线![]() 的斜率为
的斜率为![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,
,
由题知![]() ,
,![]() 联立
联立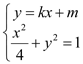 ,得
,得![]()
![]() .
.
∴![]() ,
,![]()
![]() ,由题意知
,由题意知![]() ,
,
∴![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,可得
,可得![]()
![]() ,∴
,∴![]() ,即
,即![]() .
.
因此存在常数![]() 使得结论成立.
使得结论成立.

练习册系列答案
相关题目
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.